 por cardosor23 » Ter Mai 22, 2012 09:27
por cardosor23 » Ter Mai 22, 2012 09:27
Bom dia,
Relativamente à sucessão
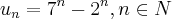
a. un coincide com a sucessão vn definida por v0 = 0, v1= 5, v2=45,
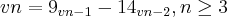
b. Cada termo un da sucessão é divisível por 5.
Tem-se que:
a. Ambas as afirmações são falsas
b. A afirmação a é verdadeira, mas a afirmação b é falsa
c. A afirmação b é verdadeira, mas a afirmação a é falsa.
d. Ambas são verdadeiras.
Abraço.
-
cardosor23
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 26, 2012 19:26
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: cursando
 por fraol » Sáb Mai 26, 2012 01:29
por fraol » Sáb Mai 26, 2012 01:29
Ambas são verdadeiras.
Você pode chegar a essa conclusão usando o Princípio da Indução Finita (PIF) em ambas as alternativas assim:
Item a)
Claramente

.
Suponha que

.
Desenvolva
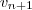
usando a definição do termo geral de
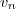
dada no enunciado e
fazendo a substituição adequada da hipótese

.
Você vai chegar em

o que mostra que

e
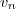
são coincidentes

.
Item b)
Use o PIF da forma convencional.
Tenta aí, qualquer coisa manda pra cá.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
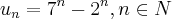
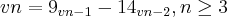


 .
. .
.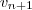 usando a definição do termo geral de
usando a definição do termo geral de 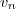 dada no enunciado e
dada no enunciado e  o que mostra que
o que mostra que  e
e  .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.