 por Claudin » Dom Mai 13, 2012 12:43
por Claudin » Dom Mai 13, 2012 12:43
Determine o centro, os vértices e os focos da elipse
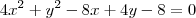
Reduzindo a equação encontrei:
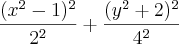
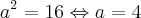
logo,

(Eixo Maior)

logo,

(Eixo Menor)
![a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3} a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3}](/latexrender/pictures/24871e492b7e1a72d83cf46caef3de5d.png)
logo,
![F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3} F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3}](/latexrender/pictures/655d5c44d05a84ca22485d2be9e01bf6.png)
![e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2} e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2}](/latexrender/pictures/9ad7d03db6662451ecc8bb28ef368612.png)
Portanto:
![F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3}) F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3})](/latexrender/pictures/6f2d35ea939a773dfd996f7addd7cefc.png)
![F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3}) F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3})](/latexrender/pictures/31ccee643396e87cd8f4feaa7f4cc6d8.png)
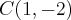
ou

Não sei direito qual o certo.
E os valores de

e

também não consegui encontrar.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Dom Mai 13, 2012 13:05
por Claudin » Dom Mai 13, 2012 13:05
Outra dúvida também seria o seguinte:

ou


ou
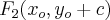
Gostaria de saber quando se usa um ou o outro, ou se essa ordem não altera em nada?!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Dom Mai 20, 2012 16:03
por Claudin » Dom Mai 20, 2012 16:03
?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Dom Mai 20, 2012 18:39
por DanielFerreira » Dom Mai 20, 2012 18:39
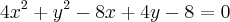
================>
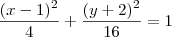
Para encontrar o centro faça:
x - 1 = 0
x = 1y + 2 = 0
y = - 2Centro (1, - 2) Para encontrar os vétices devemos primeiro achar os eixos:
Marque o centro (1, - 2) da elipse no gráfico cartesiano, agora, marque o eixo maior e o eixo menor no gráfico com relação ao centro (1, - 2). Então, una os vértices.
Agora, olhe para o gráfico e determine os pontos com relação ao centro (0, 0).
Vértices:
(- 1, - 2); (3, - 2); (1, 2) e (1, - 6)Vale rassaltar que, a elipse cujo denominador é maior terá eixo maior na variável do seu numerador; nesse caso, o eixo maior está em "y", por isso a equação será:

========>


=====>

=====>

Daí,
![c = 2\sqrt[]{3} c = 2\sqrt[]{3}](/latexrender/pictures/e5fdf170109e325b5b5ec3b1b6448b34.png)
e
![c = - 2\sqrt[]{3} c = - 2\sqrt[]{3}](/latexrender/pictures/6fd996dda7a1838987ee0a9527682098.png)
Como sabemos que o eixo maior está em y, o foco será dado por:
![(1, - 2\sqrt[]{3}) (1, - 2\sqrt[]{3})](/latexrender/pictures/3b1a2c2c81e72983e0f05ee4d0bcae6e.png)
e
![(1, 2\sqrt[]{3}) (1, 2\sqrt[]{3})](/latexrender/pictures/38b7253682996bd9ca117ce153b1ad09.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Claudin » Dom Mai 20, 2012 18:52
por Claudin » Dom Mai 20, 2012 18:52
Os focos não seriam:
![(1,-2+2\sqrt[]{3}) (1,-2+2\sqrt[]{3})](/latexrender/pictures/e36818cc89a8e23200a67376c93f297c.png)
![(1,-2-2\sqrt[]{3}) (1,-2-2\sqrt[]{3})](/latexrender/pictures/734aaba5806486a77f0164b1cd96fe41.png)
E ainda não consegui entender como chegar nesses resultados dos vértices, não sei como encontrar.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Dom Mai 20, 2012 18:56
por DanielFerreira » Dom Mai 20, 2012 18:56
Claudin escreveu:Os focos não seriam:
![(1,-2+2\sqrt[]{3}) (1,-2+2\sqrt[]{3})](/latexrender/pictures/e36818cc89a8e23200a67376c93f297c.png)
![(1,-2-2\sqrt[]{3}) (1,-2-2\sqrt[]{3})](/latexrender/pictures/734aaba5806486a77f0164b1cd96fe41.png)
E ainda não consegui entender como chegar nesses resultados dos vértices, não sei como encontrar.
Tens razão!
Vou desenhar aqui a figura, aí vc tenta seguir o que falei, vlw??
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Mai 20, 2012 19:13
por DanielFerreira » Dom Mai 20, 2012 19:13
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Claudin » Dom Mai 20, 2012 23:08
por Claudin » Dom Mai 20, 2012 23:08
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1524 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
-
- Conicas
por baianinha » Qua Set 14, 2011 00:30
- 1 Respostas
- 1431 Exibições
- Última mensagem por LuizAquino

Qua Set 14, 2011 00:58
Álgebra Elementar
-
- Cônicas
por Claudin » Dom Mai 13, 2012 14:34
- 5 Respostas
- 2231 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 20:03
Geometria Analítica
-
- Cônicas
por Claudin » Dom Mai 13, 2012 14:35
- 7 Respostas
- 2996 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 17:34
Geometria Analítica
-
- Cônicas
por Claudin » Dom Mai 13, 2012 14:37
- 3 Respostas
- 1519 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 10:16
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
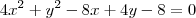
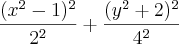
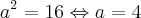 logo,
logo,  (Eixo Maior)
(Eixo Maior) logo,
logo,  (Eixo Menor)
(Eixo Menor)![a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3} a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3}](/latexrender/pictures/24871e492b7e1a72d83cf46caef3de5d.png) logo,
logo, ![F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3} F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3}](/latexrender/pictures/655d5c44d05a84ca22485d2be9e01bf6.png)
![e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2} e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2}](/latexrender/pictures/9ad7d03db6662451ecc8bb28ef368612.png)
![F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3}) F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3})](/latexrender/pictures/6f2d35ea939a773dfd996f7addd7cefc.png)
![F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3}) F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3})](/latexrender/pictures/31ccee643396e87cd8f4feaa7f4cc6d8.png)
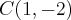 ou
ou  Não sei direito qual o certo.
Não sei direito qual o certo. e
e  também não consegui encontrar.
também não consegui encontrar.
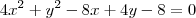
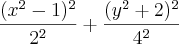
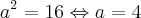 logo,
logo,  (Eixo Maior)
(Eixo Maior) logo,
logo,  (Eixo Menor)
(Eixo Menor)![a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3} a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3}](/latexrender/pictures/24871e492b7e1a72d83cf46caef3de5d.png) logo,
logo, ![F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3} F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3}](/latexrender/pictures/655d5c44d05a84ca22485d2be9e01bf6.png)
![e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2} e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2}](/latexrender/pictures/9ad7d03db6662451ecc8bb28ef368612.png)
![F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3}) F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3})](/latexrender/pictures/6f2d35ea939a773dfd996f7addd7cefc.png)
![F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3}) F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3})](/latexrender/pictures/31ccee643396e87cd8f4feaa7f4cc6d8.png)
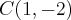 ou
ou  Não sei direito qual o certo.
Não sei direito qual o certo. e
e  também não consegui encontrar.
também não consegui encontrar.
 ou
ou 
 ou
ou 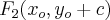


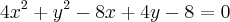 ================>
================> 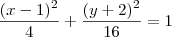
 ========>
========> 
 =====>
=====>  =====>
=====> 
![c = 2\sqrt[]{3} c = 2\sqrt[]{3}](/latexrender/pictures/e5fdf170109e325b5b5ec3b1b6448b34.png) e
e ![c = - 2\sqrt[]{3} c = - 2\sqrt[]{3}](/latexrender/pictures/6fd996dda7a1838987ee0a9527682098.png)
![(1, - 2\sqrt[]{3}) (1, - 2\sqrt[]{3})](/latexrender/pictures/3b1a2c2c81e72983e0f05ee4d0bcae6e.png) e
e ![(1, 2\sqrt[]{3}) (1, 2\sqrt[]{3})](/latexrender/pictures/38b7253682996bd9ca117ce153b1ad09.png)

![(1,-2+2\sqrt[]{3}) (1,-2+2\sqrt[]{3})](/latexrender/pictures/e36818cc89a8e23200a67376c93f297c.png)
![(1,-2-2\sqrt[]{3}) (1,-2-2\sqrt[]{3})](/latexrender/pictures/734aaba5806486a77f0164b1cd96fe41.png)



