Meu professor passou um problema para resolver que ao você montar fica um sistema de 2 equações mas 3 incognitas!!! Tentei fazer Cramer, Escalonamento, O método da comparação, mas, não consegui resolver cheguei até a ficar com uma equação de 2 incognitas!!!
Cheguei a montar o sistema mas não consegui resolver meu sistema ficou assim:
3x+7y+z=42,1
4x+10y+z=47,3
Mas, não consegui resolver!!!
Problema:
Uma loja vende 3 tipos de lampadas (x,y,z. Tamara comprou 3 lampadas tipo x, 7 tipo y, e 1 tipo z, pagando R$42,10. José comprou 4 lampadas tipo x, 10 tipo y e uma tipo z, pagando R$47,30. Nas condições dadas, a compra de 3 lampadas, sendo uma de cada tipo custa:
a) R$ 30,50 b) R$ 31,40 c) R$ 31,70 d) 32,30 e)R$33,20
============================> 
===========================> 
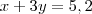
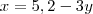
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.