 por cafinfa » Dom Mai 20, 2012 16:43
por cafinfa » Dom Mai 20, 2012 16:43
(5 elevado a (x mais 4) vezes 5 elevado a 3x) tudo isso sobre 5 elevado a (4x mais 5). me ajudem por favor eu tentei mas não consegui
-
cafinfa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 20, 2012 16:37
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Dom Mai 20, 2012 16:56
por Molina » Dom Mai 20, 2012 16:56
Boa tarde.
cafinfa escreveu:(5 elevado a (x mais 4) vezes 5 elevado a 3x) tudo isso sobre 5 elevado a (4x mais 5). me ajudem por favor eu tentei mas não consegui
Primeiramente, seja bem-vindo ao AjudaMatemática.
Para evitar este tipo de escrita, nós disponibilizamos um
Editor de Fórmulas onde você pode fazer uma melhor edição de suas sentenças matemáticas.
Quanto a sua dúvida, confirme se é isso:
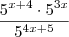
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cafinfa » Dom Mai 20, 2012 17:06
por cafinfa » Dom Mai 20, 2012 17:06
sim, obrigado
-
cafinfa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 20, 2012 16:37
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Dom Mai 20, 2012 17:19
por Molina » Dom Mai 20, 2012 17:19
cafinfa escreveu:sim, obrigado
Na verdade o que você está pretendendo não é racionalizar denominadores, e sim simplificar esta fração utilizando as propriedades da potenciação. Racionalização é outro assunto. Mas vamos la...
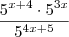
Utilizando a propriedade da multiplicação de potência com as mesmas bases, somamos os expoentes:

Utilizando a propriedade da divisão de potência com as mesmas bases, subtraímos os expoentes:

Resolvendo o expoente:

Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- racionalização de denominadores
por Claudia Silva » Qua Jun 22, 2011 21:15
- 1 Respostas
- 1750 Exibições
- Última mensagem por FilipeCaceres

Qua Jun 22, 2011 22:10
Álgebra Elementar
-
- Racionalização de denominadores
por LuizCarlos » Qua Mai 09, 2012 15:10
- 2 Respostas
- 1819 Exibições
- Última mensagem por LuizCarlos

Qua Mai 09, 2012 18:54
Álgebra Elementar
-
- racionalização de denominadores
por cafinfa » Dom Mai 20, 2012 17:16
- 1 Respostas
- 1409 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:21
Álgebra Elementar
-
- Racionalização de denominadores
por Tibinhas » Seg Jun 25, 2012 19:24
- 3 Respostas
- 2764 Exibições
- Última mensagem por Arkanus Darondra

Sáb Jul 07, 2012 22:29
Álgebra Elementar
-
- Racionalização de denominadores
por Thais Aquino Lima » Ter Fev 12, 2013 08:07
- 1 Respostas
- 1213 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 11:17
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



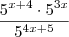


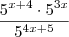





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.