 por matematicouff » Ter Mai 15, 2012 14:31
por matematicouff » Ter Mai 15, 2012 14:31
Como mostro que essa função admite inversa?
- Mostre que a função
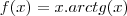
admite inversa no intervalo
![(-\infty,0] (-\infty,0]](/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png)
, e use o Teorema da Função Inversa para calcular

.
-
matematicouff
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 29, 2012 15:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sex Mai 18, 2012 19:54
por LuizAquino » Sex Mai 18, 2012 19:54
matematicouff escreveu:Como mostro que essa função admite inversa?
- Mostre que a função
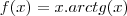
admite inversa no intervalo
![(-\infty,0] (-\infty,0]](/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png)
, e use o Teorema da Função Inversa para calcular

.
Sabemos que:
Se f é estritamente crescente ou estritamente decresencente em seu domínio, então f é inversível.
Lembrando que uma função é estritamente crescente em [a, b] quando
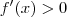
para todo x em [a, b]. Por outro lado, uma função é estritamente decrescente em [a, b] quando
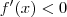
para todo x em [a, b].
Agora tente usar essas informações.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por matematicouff » Dom Mai 20, 2012 04:47
por matematicouff » Dom Mai 20, 2012 04:47
Ok, derivei a função e deu o seguinte:

.
Analizando o sinal dessa função, vemos que ela é negativa em todo o intervalo
![(-\infty, 0] ==> (-\infty, 0] ==>](/latexrender/pictures/765749b8808879ca2f291b2971349875.png)
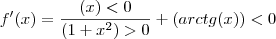
. Logo, f é decrescente nesse intervalo e então admite inversa.
Empaquei agora foi na derivada. Poderia me ajudar?
-
matematicouff
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 29, 2012 15:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Dom Mai 20, 2012 21:39
por LuizAquino » Dom Mai 20, 2012 21:39
matematicouff escreveu:Ok, derivei a função e deu o seguinte:

.
Ok.
matematicouff escreveu:Analizando o sinal dessa função, vemos que ela é negativa em todo o intervalo
![(-\infty, 0] ==> (-\infty, 0] ==>](/latexrender/pictures/765749b8808879ca2f291b2971349875.png)
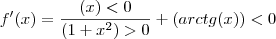
. Logo, f é decrescente nesse intervalo e então admite inversa.
Cuidado! O intervalo que você escreveu inclui o zero. Note que para x = 0 a derivada é nula, e não negativa como você afirma.
Sendo assim, primeiro você pode afirmar que a função
f é estritamente decrescente em

.
Em seguida, usando a continuidade de
f, você pode incluir o zero nesse intervalo e dizer que ela ainda é estritamente decrescente em
![(-\infty,\, 0] (-\infty,\, 0]](/latexrender/pictures/1343a962d509cd11242dfc8c7ae0c7e9.png)
.
matematicouff escreveu:Empaquei agora foi na derivada. Poderia me ajudar?
Pelo Teorema da Função Inversa, temos que:

Note que você já calculou
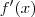
. Basta agora avaliá-la em x = -1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3401 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- O que é função inversa
por irineu junior » Sex Mar 12, 2010 20:57
- 2 Respostas
- 2644 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 16:28
Funções
-
- Função Inversa
por OtavioBonassi » Qui Jul 14, 2011 23:04
- 6 Respostas
- 7731 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:14
Funções
-
- Função Inversa.
por jcvalim » Qua Ago 24, 2011 15:57
- 0 Respostas
- 1186 Exibições
- Última mensagem por jcvalim

Qua Ago 24, 2011 15:57
Funções
-
- função inversa
por tigre matematico » Qui Out 13, 2011 12:45
- 1 Respostas
- 2213 Exibições
- Última mensagem por Guill

Sáb Abr 21, 2012 18:07
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
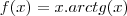 admite inversa no intervalo
admite inversa no intervalo ![(-\infty,0] (-\infty,0]](/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png) , e use o Teorema da Função Inversa para calcular
, e use o Teorema da Função Inversa para calcular  .
.
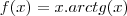 admite inversa no intervalo
admite inversa no intervalo ![(-\infty,0] (-\infty,0]](/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png) , e use o Teorema da Função Inversa para calcular
, e use o Teorema da Função Inversa para calcular  .
.
admite inversa no intervalo
, e use o Teorema da Função Inversa para calcular
.
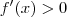 para todo x em [a, b]. Por outro lado, uma função é estritamente decrescente em [a, b] quando
para todo x em [a, b]. Por outro lado, uma função é estritamente decrescente em [a, b] quando 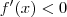 para todo x em [a, b].
para todo x em [a, b].
 .
. ![(-\infty, 0] ==> (-\infty, 0] ==>](/latexrender/pictures/765749b8808879ca2f291b2971349875.png)
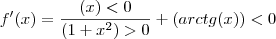 . Logo, f é decrescente nesse intervalo e então admite inversa.
. Logo, f é decrescente nesse intervalo e então admite inversa.
.
![(-\infty, 0] ==> (-\infty, 0] ==>](/latexrender/pictures/765749b8808879ca2f291b2971349875.png)
. Logo, f é decrescente nesse intervalo e então admite inversa.
 .
.![(-\infty,\, 0] (-\infty,\, 0]](/latexrender/pictures/1343a962d509cd11242dfc8c7ae0c7e9.png) .
.
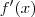 . Basta agora avaliá-la em x = -1.
. Basta agora avaliá-la em x = -1.