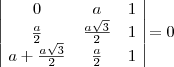por Larice Mourao » Qui Mai 17, 2012 15:44
por Larice Mourao » Qui Mai 17, 2012 15:44
(Fuvest)No plano cartesiano, considere o quadrado de vértices A= (0,0) , B = (a,0), C (0,a) e D (a,a), onde a>0. sabendo-se que os triângulos ABE, com E no interior do quadrado, e BDF, com F no exterior do quadrado, são triângulos equiláteros, prove que os pontos C, E e F estão alinhados.
eu sei que para que não exista triangulo o determinante é igual a zero e assim os pontos estão alinhados . Mas como poder haver triangulo (determinante diferente de zero , eu suponho) se os pontos estão alinhados (determinante igual a zero) ?? com essa dúvida nao consigo nem montar o determinante ... Bem , eu não consegui , se alguém puder me orientar fico muito grata ...
-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sáb Mai 19, 2012 16:06
por LuizAquino » Sáb Mai 19, 2012 16:06
Larice Mourao escreveu:(Fuvest)No plano cartesiano, considere o quadrado de vértices A= (0,0) , B = (a,0), C (0,a) e D (a,a), onde a>0. sabendo-se que os triângulos ABE, com E no interior do quadrado, e BDF, com F no exterior do quadrado, são triângulos equiláteros, prove que os pontos C, E e F estão alinhados.
Larice Mourao escreveu:eu sei que para que não exista triangulo o determinante é igual a zero e assim os pontos estão alinhados . Mas como poder haver triangulo (determinante diferente de zero , eu suponho) se os pontos estão alinhados (determinante igual a zero) ?? com essa dúvida nao consigo nem montar o determinante ... Bem , eu não consegui , se alguém puder me orientar fico muito grata ...
Você está confundindo os conceitos. Note que o exercício pede que seja provado que C, E e F estão alinhados. Em outras palavras, CEF não forma um triângulo. Entretanto, não há problema algum em ABE e BDF serem triângulos.
A figura abaixo ilustra o exercício.

- figura.png (5.4 KiB) Exibido 4806 vezes
Analisando essa figura, como ABE e BDF são triângulos equiláteros, note que:

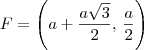
Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Larice Mourao » Dom Mai 20, 2012 04:08
por Larice Mourao » Dom Mai 20, 2012 04:08
Luis Aquino , sério , chorei de emoção aqui , muitíssimo obrigada ..
Mas nem sei se acertei , o meu livro não tem a resposta .
O resultado que eu encontrei foi 3a²=0 , acho que errei em alguma parte , eu fiz o determinante com o valor do ponto C abaixo o do E e abaixo com o do F mais uma coluna com 1 , aplicando a regra de Sarrus .. e igualando a zero . :(
mas , mais uma vez , Muito obrigada !!

-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Larice Mourao » Dom Mai 20, 2012 04:26
por Larice Mourao » Dom Mai 20, 2012 04:26
Desculpe-me eu refiz o cálculo e deu certo , realmente o resultado é zero , kkkk, que burra eu . Ficam 5a²-5a²+2a²raiz²(aindanão aprendi em latex)de 3 - 2a² raiz ² de 3. Você esclareceu mesmo , Valeeeeeeu!!
-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Dom Mai 20, 2012 20:49
por LuizAquino » Dom Mai 20, 2012 20:49
Larice Mourao escreveu:Luiz Aquino , sério , chorei de emoção aqui , muitíssimo obrigada ..
Mas nem sei se acertei , o meu livro não tem a resposta .
O resultado que eu encontrei foi 3a²=0 , acho que errei em alguma parte , eu fiz o determinante com o valor do ponto C abaixo o do E e abaixo com o do F mais uma coluna com 1 , aplicando a regra de Sarrus .. e igualando a zero . :(
mas , mais uma vez , Muito obrigada !!

Larice Mourao escreveu:Desculpe-me eu refiz o cálculo e deu certo , realmente o resultado é zero , kkkk, que burra eu . Ficam 5a²-5a²+2a²raiz²(aindanão aprendi em latex)de 3 - 2a² raiz ² de 3. Você esclareceu mesmo , Valeeeeeeu!!
O que aparece no resultado do determinante não é essa expressão. Ainda falta o número 4, que aparece dividindo.
Note que você deseja calcular o determinante:
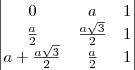
Veja que eu
não igualei esse determinante a zero ainda. Na verdade, primeiro eu tenho que
calcular esse determinante. Só no final das contas, se esse determinante for igual a zero, é que poderemos dizer que os pontos estão alinhados.
Aplicando a Regra de Sarrus, temos que:

![= \left[0\cdot \frac{a\sqrt{3}}{2} \cdot 1 + a\cdot 1 \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 1\cdot \frac{a}{2}\cdot \frac{a}{2}\right] - \left[1\cdot \frac{a\sqrt{3}}{2} \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 0 \cdot 1 \cdot \frac{a}{2} + a\cdot \frac{a}{2}\cdot 1\right] = \left[0\cdot \frac{a\sqrt{3}}{2} \cdot 1 + a\cdot 1 \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 1\cdot \frac{a}{2}\cdot \frac{a}{2}\right] - \left[1\cdot \frac{a\sqrt{3}}{2} \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 0 \cdot 1 \cdot \frac{a}{2} + a\cdot \frac{a}{2}\cdot 1\right]](/latexrender/pictures/7a55eaed875389280ed08f6aeaa0d29e.png)



Agora sim podemos dizer que:
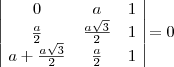
Sendo assim, os pontos estão alinhados.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Larice Mourao » Ter Mai 22, 2012 23:49
por Larice Mourao » Ter Mai 22, 2012 23:49
aaa verdade . Eu conferi aqui , percebi que não havia multiplicado o denominador do 3a² , tinha deixado apenas o 2 no denominador , aí qnd fiz o mmc o numerador ficou multiplicado por 2.. realmente se fosse prova aberta tinha errado :ss Obrigada por conferir a resposta !!! viajeeei desde o começo da questão ... rsrs
-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Alinhamento de três pontos] SEM SER POR MATRIZ
por vitor_jo » Qua Jan 14, 2015 05:40
- 3 Respostas
- 10304 Exibições
- Última mensagem por vitor_jo

Qua Jan 14, 2015 18:47
Geometria Analítica
-
- [pontos/área] Geometria Analítica
por Isaa » Qua Set 10, 2008 18:18
- 2 Respostas
- 4175 Exibições
- Última mensagem por Isaa

Qui Set 11, 2008 13:05
Geometria Analítica
-
- [Geometria Analítica] Pontos no espaço tridimensional
por Ronaldobb » Seg Dez 02, 2013 23:19
- 1 Respostas
- 1506 Exibições
- Última mensagem por e8group

Qua Dez 04, 2013 18:01
Geometria Analítica
-
- [Geometria Analítica] distância entre pontos
por aprendiz007 » Sex Dez 02, 2016 17:58
- 0 Respostas
- 2606 Exibições
- Última mensagem por aprendiz007

Sex Dez 02, 2016 17:58
Geometria Analítica
-
- [Geometria Analítica] Área formada por pontos no plano
por acorreia » Ter Mai 08, 2012 18:05
- 1 Respostas
- 1785 Exibições
- Última mensagem por LuizAquino

Ter Mai 08, 2012 20:36
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



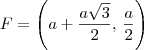


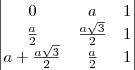

![= \left[0\cdot \frac{a\sqrt{3}}{2} \cdot 1 + a\cdot 1 \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 1\cdot \frac{a}{2}\cdot \frac{a}{2}\right] - \left[1\cdot \frac{a\sqrt{3}}{2} \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 0 \cdot 1 \cdot \frac{a}{2} + a\cdot \frac{a}{2}\cdot 1\right] = \left[0\cdot \frac{a\sqrt{3}}{2} \cdot 1 + a\cdot 1 \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 1\cdot \frac{a}{2}\cdot \frac{a}{2}\right] - \left[1\cdot \frac{a\sqrt{3}}{2} \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 0 \cdot 1 \cdot \frac{a}{2} + a\cdot \frac{a}{2}\cdot 1\right]](/latexrender/pictures/7a55eaed875389280ed08f6aeaa0d29e.png)