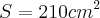Estou com dúvida nesse!
Em alguns triângulos a medida do lado tem
 unidade a mais do que a medida da altura relativa a este lado.
unidade a mais do que a medida da altura relativa a este lado.a) Expresse a área desses triângulos em função da medida do lado considerado.
Resposta:
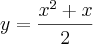
b) Calcule a área de um triângulo desse tipo, cuja altura mede
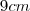 .
.Resposta:
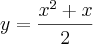
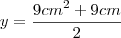
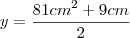
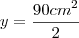
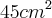
c) Se a medida do lado de um triângulo desse tipo for
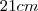 ,qual será a área do triângulo.
,qual será a área do triângulo.Resposta:
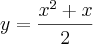
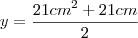
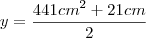
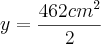
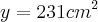
Onde estou errando essa questão c, pois no livro a resposta é:
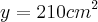 .
. 


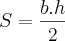 ;
;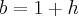 , ou
, ou 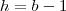
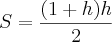 ========= em função da altura ======>
========= em função da altura ======> 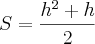
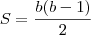 ============ em função do lado ======>
============ em função do lado ======> 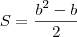

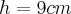
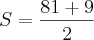 ====>
====> 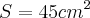
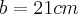
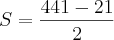 ====>
====>