Estou estudando derivadas parciais. Porém agora estou com uma dúvida na seguinte função:
Como a função está com exponecial eu não consigo resolve-la.
A professo faz assim:
Semelhante a integração por substituição, ai no du, ela derivada na ordem de apenas uma variável. Ai fica:
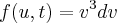
Ai então ela retorna com os valores:
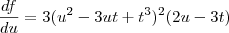
E faz o mesmo com as outras ordens.
Mas está correto isso? Minha dúvida é porque não encontrei material falando de "Derivada por substituição".
Caso não esteja correto, se alguém puder, mostrar a forma correta agradeceria muito.
Bom dia e bons estudos!
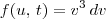. Provavelmente ele escreve apenas 
. O termo dv será escrito apenas na derivada. Ou seja, irá aparecer em 
.
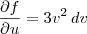por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)