por kaaps » Sáb Mai 12, 2012 20:54
OLá !
Eu estou com um problema na resolução de um exercício usando a Regra de Simpson.
Só tenho 1 folha a explicar mais ou menos como aplico a regra mas assim fica complicado.
O problema que tenho é.
Com a Função F(x)=x^5+x^4-2x^3-1
Com o Intervalo [-2,-1]
e com o Integral
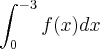
Considerando 4 subintervalor
Resolver este exercício usando a Regra de Simpson !
Alguém me pode dar uma ajuda ?
Obrigado Cumprimentos (:
-
kaaps
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Sáb Mai 12, 2012 20:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Computação Gráfica e Multimédia
- Andamento: cursando
por LuizAquino » Seg Mai 14, 2012 09:21
kaaps escreveu:OLá !
Eu estou com um problema na resolução de um exercício usando a Regra de Simpson.
Só tenho 1 folha a explicar mais ou menos como aplico a regra mas assim fica complicado.
O problema que tenho é.
Com a Função F(x)=x^5+x^4-2x^3-1
Com o Intervalo [-2,-1]
e com o Integral
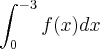
Considerando 4 subintervalor
Resolver este exercício usando a Regra de Simpson !
Alguém me pode dar uma ajuda?
Qual foi exatamente a sua dificuldade? O que você já tentou fazer?
Lembre-se que uma das
Regras deste fórum (a Regra 1) é exatamente informar suas tentativas e dificuldades.
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Regra de L'Hôpital] Ajuda
por Ronaldobb » Ter Nov 06, 2012 21:43
- 2 Respostas
- 1551 Exibições
- Última mensagem por MarceloFantini
Ter Nov 06, 2012 23:41
Cálculo: Limites, Derivadas e Integrais
-
- Regra de Três - ajuda
por shorboltsky » Qui Abr 25, 2013 20:13
- 1 Respostas
- 4356 Exibições
- Última mensagem por Rafael16
Qui Abr 25, 2013 23:31
Álgebra Elementar
-
- Regra de 3 Ajuda com recurso
por deividchou » Seg Ago 31, 2015 19:56
- 2 Respostas
- 2173 Exibições
- Última mensagem por deividchou
Ter Set 01, 2015 10:04
Álgebra Linear
-
- [regra do quociente] ajuda por favor
por ricardosanto » Seg Abr 16, 2012 12:26
- 4 Respostas
- 2161 Exibições
- Última mensagem por LuizAquino
Ter Abr 17, 2012 11:06
Cálculo: Limites, Derivadas e Integrais
-
- [Regra de Cramer] Precisando de ajuda!
por brunock » Ter Mai 22, 2012 16:14
- 1 Respostas
- 2077 Exibições
- Última mensagem por DanielFerreira
Dom Mai 27, 2012 15:04
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
