


rafaelbr91 escreveu:Bem, eu queria saber como vou fazer o esboço gráfico da função f(x)= x³-2x+3x , o problema consiste no momento em que vou achar o ponto crítico da função, pois as raízes de f '(x), que corresponde à, 3x²-4x+3, são raízes complexas, dai eu n sei como representálas no gráfico( a dúvida é em relação a complexos então..), as raízes são : x' = 0,66 + 0,74.i e x" = 0,66 - 0,74.i Como represento elas graficamente? Agradecido.
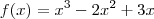 e não
e não  como você escreveu.
como você escreveu.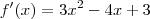 . Como suas raízes são complexas e a concavidade da parábola é para cima, temos que
. Como suas raízes são complexas e a concavidade da parábola é para cima, temos que 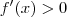 para todo x.
para todo x.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante