tenho a equação f(x)=x³-2x+1 e preciso encontrar suas raizes.
como faço?



spyderkill escreveu:tenho a equação f(x)=x³-2x+1 e preciso encontrar suas raizes.
como faço?
 . Nesse caso, essa seria uma equação polinomial do 3° grau. Para achar as suas raízes, comece aplicando o Teorema das Raízes Racionais para verificar se há alguma raiz racional.
. Nesse caso, essa seria uma equação polinomial do 3° grau. Para achar as suas raízes, comece aplicando o Teorema das Raízes Racionais para verificar se há alguma raiz racional.
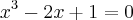
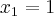

 por
por  temos:
temos: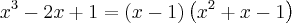


![{x}_{2}=\frac{1+\sqrt[2]{5}}{2} {x}_{2}=\frac{1+\sqrt[2]{5}}{2}](/latexrender/pictures/4ebd4cfe7a308c867f65f2645953d218.png) e
e ![{x}_{3}=\frac{1-\sqrt[2]{5}}{2} {x}_{3}=\frac{1-\sqrt[2]{5}}{2}](/latexrender/pictures/ef5fcd113f7df7a92fb26c0858b55cf2.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)