acorreia escreveu:Considere o conjunto C dos pontos do plano euclidiano que satisfazem simultaneamente as seguintes equações:
y >= -x - 1
y <= x + 6
Y >= x - 3
y <= -x + 2
Sabendo que a fórmula da área de um retângulo de altura H e largura B é BxH, encontre a área do conjunto C.
Você sabe fazer o esboço de uma reta a partir de sua equação? Por exemplo, você sabe fazer o esboço da reta y = - x - 1?
Se você souber, então lembre-se que
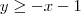
significa todos os pontos que estão acima e sobre a reta y = -x - 1.
Por outro lado, lembre-se que

significa todos os pontos que estão abaixo e sobre a reta y = x + 6.
Considerando essas informações, tente fazer o exercício. Se você não conseguir terminar, então poste aqui até que ponto você conseguiu desenvolver.
Caso você não saiba fazer o esboço de uma reta, eu recomendo que você assista a videoaula "Matemática - Aula 4 - Função do Primeiro Grau". Ela está disponível no canal do Nerckie no YouTube:
http://www.youtube.com/nerckie

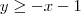 significa todos os pontos que estão acima e sobre a reta y = -x - 1.
significa todos os pontos que estão acima e sobre a reta y = -x - 1. significa todos os pontos que estão abaixo e sobre a reta y = x + 6.
significa todos os pontos que estão abaixo e sobre a reta y = x + 6.

 .
.



