 por LuizCarlos » Seg Mai 07, 2012 19:42
por LuizCarlos » Seg Mai 07, 2012 19:42
Olá amigos, estou com uma dúvida nessa questão:
![\sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} = \sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} =](/latexrender/pictures/7c8eebb76cd7de2c3ae51e2d9916062e.png)
![\sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})} \sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})}](/latexrender/pictures/434ff9896760ac044dd3c4e2952021df.png)
![2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})= 2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})=](/latexrender/pictures/ba2013068c53ebf2f753985ef101bd3b.png)
Os expoentes

e
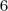
estão elevando as frações!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Seg Mai 07, 2012 20:56
por Molina » Seg Mai 07, 2012 20:56
Boa noite, Luiz Carlos.
LuizCarlos escreveu:Olá amigos, estou com uma dúvida nessa questão:
![\sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} = \sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} =](/latexrender/pictures/7c8eebb76cd7de2c3ae51e2d9916062e.png)
![\sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})} \sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})}](/latexrender/pictures/434ff9896760ac044dd3c4e2952021df.png)
![2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})= 2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})=](/latexrender/pictures/ba2013068c53ebf2f753985ef101bd3b.png)
Os expoentes

e
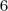
estão elevando as frações!
Dando uma formatada na sua expressão temos:
![2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 } 2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 }](/latexrender/pictures/b846f31db7e7d74ac43727f3e09fec3f.png)
Perceba que:
![2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 } = 2 \cdot \sqrt[15]{\left(\frac{3^{10}}{2^5} \right) \cdot \left(\frac{2^6}{3^9} \right) } 2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 } = 2 \cdot \sqrt[15]{\left(\frac{3^{10}}{2^5} \right) \cdot \left(\frac{2^6}{3^9} \right) }](/latexrender/pictures/0f3c9b818bf03c3b5493e6b8ec80bd3c.png)
Consegue seguir a partir daqui?
Use as propriedades de potenciação e radiciação.
Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 3300 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2341 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais
por Andrewo » Qua Fev 01, 2012 13:43
- 8 Respostas
- 4134 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 12:22
Álgebra Elementar
-
- Radicais II
por Andrewo » Qui Fev 09, 2012 19:38
- 3 Respostas
- 1884 Exibições
- Última mensagem por MarceloFantini

Sex Fev 10, 2012 11:32
Álgebra Elementar
-
- Radicais de nv
por Andrewo » Seg Fev 13, 2012 16:58
- 4 Respostas
- 2465 Exibições
- Última mensagem por Arkanus Darondra

Ter Fev 14, 2012 13:01
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} = \sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} =](/latexrender/pictures/7c8eebb76cd7de2c3ae51e2d9916062e.png)
![\sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})} \sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})}](/latexrender/pictures/434ff9896760ac044dd3c4e2952021df.png)
![2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})= 2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})=](/latexrender/pictures/ba2013068c53ebf2f753985ef101bd3b.png)
 e
e 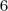 estão elevando as frações!
estão elevando as frações!
![\sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} = \sqrt[3]{\frac{9}{2}} . 2\sqrt[5]{\frac{4}{27}} =](/latexrender/pictures/7c8eebb76cd7de2c3ae51e2d9916062e.png)
![\sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})} \sqrt[15]{{(\frac{9}{2})}^{5}} .2\sqrt[15]{({\frac{4}{27}}^{3})}](/latexrender/pictures/434ff9896760ac044dd3c4e2952021df.png)
![2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})= 2.\sqrt[15]{({\frac{9}{2}}^{5})}}.({\frac{4}{27}}^{3})=](/latexrender/pictures/ba2013068c53ebf2f753985ef101bd3b.png)
 e
e 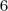 estão elevando as frações!
estão elevando as frações!
e
estão elevando as frações!
![2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 } 2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 }](/latexrender/pictures/b846f31db7e7d74ac43727f3e09fec3f.png)
![2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 } = 2 \cdot \sqrt[15]{\left(\frac{3^{10}}{2^5} \right) \cdot \left(\frac{2^6}{3^9} \right) } 2 \cdot \sqrt[15]{\left(\frac{9}{2} \right)^5 \cdot \left(\frac{4}{27} \right)^3 } = 2 \cdot \sqrt[15]{\left(\frac{3^{10}}{2^5} \right) \cdot \left(\frac{2^6}{3^9} \right) }](/latexrender/pictures/0f3c9b818bf03c3b5493e6b8ec80bd3c.png)




 , avisa que eu resolvo.
, avisa que eu resolvo.

