 por MarianaAlmeida » Qui Jul 09, 2009 16:51
por MarianaAlmeida » Qui Jul 09, 2009 16:51
sÓ GOSTARIA DE SABER SE ESTÁ CORRETA A MANEIRA QUE EU UTILIZEI PARA RESOLVER
exercício:
Sabendo que 2+i é uma das raízes da euqção
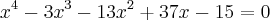
, quais as outras raizes?
resolução:
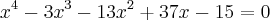
, (2+i)
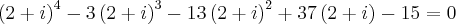
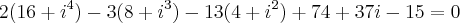
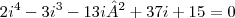
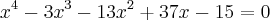
, (2-i)

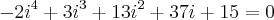
usei Briot para transforma em equação de segundo grau
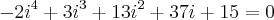
-2 +3 +13 +37 +15
-2 -2 7 -1 39 63
2 -2 3 5 49
-2x²+3x+5
passei para báskara
![{x}_{1}= \frac{-3+\sqrt[]{9-4.(-2).5}}{2.(-2)} {x}_{1}= \frac{-3+\sqrt[]{9-4.(-2).5}}{2.(-2)}](/latexrender/pictures/b33aa564460801c6c346a764361dea68.png)
![{x}_{1}= \frac{-3+\sqrt[]{49}}{-4} {x}_{1}= \frac{-3+\sqrt[]{49}}{-4}](/latexrender/pictures/577ced2e11fe223c6c8e1cbd1451a9cb.png)



![{x}_{2}= \frac{-3-\sqrt[]{9-4.(-2).5}}{2.(-2)}
[tex]{x}_{2}= \frac{-3-\sqrt[]{49}}{-4}
[tex]{x}_{2}= \frac{-3-7}{-4} {x}_{2}= \frac{-3-\sqrt[]{9-4.(-2).5}}{2.(-2)}
[tex]{x}_{2}= \frac{-3-\sqrt[]{49}}{-4}
[tex]{x}_{2}= \frac{-3-7}{-4}](/latexrender/pictures/434aa31d64e73323cb534f1a2754cec9.png)

Raizes= -1 e -5/2
-
MarianaAlmeida
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jul 09, 2009 15:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Sáb Jul 11, 2009 08:48
por Cleyson007 » Sáb Jul 11, 2009 08:48
Bom dia Mariana!
Mariana, primeiramente 2+i não é raiz deste polinômio. Quando você elevou 2+i a 4 o resultado daria -7+24i e não i^4+16.
E assim por diante... O resto deste polinômio não será nulo com este binômio, então isto implica no falado antes: não é raiz.
Por favor, confira se o problema foi digitado corretamente

Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercio resolvido
por adauto martins » Ter Abr 27, 2021 10:51
- 1 Respostas
- 8080 Exibições
- Última mensagem por adauto martins

Ter Abr 27, 2021 11:00
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em exercío sobre segmentos de retas.
por Danilo » Sáb Abr 21, 2012 21:33
- 1 Respostas
- 2233 Exibições
- Última mensagem por Danilo

Seg Abr 23, 2012 00:27
Álgebra Elementar
-
- NAO CVONSIGO RESOLVER ESTE EXERCIO ME AJUDEM POR FAVOR.
por weverton » Sex Mai 14, 2010 02:04
- 2 Respostas
- 2378 Exibições
- Última mensagem por weverton

Sáb Mai 15, 2010 16:13
Matemática Financeira
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7155 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Exercio do Intocaveis "Livro do cursinho do objetivo"
por kalong » Qua Out 24, 2012 22:29
- 3 Respostas
- 26056 Exibições
- Última mensagem por diegolopes1988

Sáb Jan 14, 2017 17:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
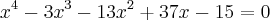 , quais as outras raizes?
, quais as outras raizes?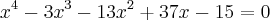 , (2+i)
, (2+i)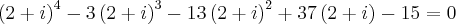
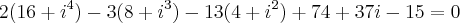
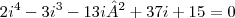
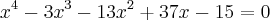 , (2-i)
, (2-i)
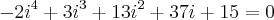
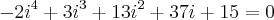
![{x}_{1}= \frac{-3+\sqrt[]{9-4.(-2).5}}{2.(-2)} {x}_{1}= \frac{-3+\sqrt[]{9-4.(-2).5}}{2.(-2)}](/latexrender/pictures/b33aa564460801c6c346a764361dea68.png)
![{x}_{1}= \frac{-3+\sqrt[]{49}}{-4} {x}_{1}= \frac{-3+\sqrt[]{49}}{-4}](/latexrender/pictures/577ced2e11fe223c6c8e1cbd1451a9cb.png)



![{x}_{2}= \frac{-3-\sqrt[]{9-4.(-2).5}}{2.(-2)}
[tex]{x}_{2}= \frac{-3-\sqrt[]{49}}{-4}
[tex]{x}_{2}= \frac{-3-7}{-4} {x}_{2}= \frac{-3-\sqrt[]{9-4.(-2).5}}{2.(-2)}
[tex]{x}_{2}= \frac{-3-\sqrt[]{49}}{-4}
[tex]{x}_{2}= \frac{-3-7}{-4}](/latexrender/pictures/434aa31d64e73323cb534f1a2754cec9.png)






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.