 por gabriel feron » Dom Mai 06, 2012 20:25
por gabriel feron » Dom Mai 06, 2012 20:25
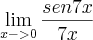
Boa noite minha duvida é a seguinte, existe o teorema do confronto, nao estudei ela ainda em aula, meus veteranos me falaram que teriamos usar pra conseguir chegar ao resultado final que é 1, mas me enrolei quando temos que transformar(derivando) sen em cos, pq? qual a logica? (nao tivemos derivada ainda, mas tenho um certo conhecimento, pq pesquisei bastante)
(sen7x)/7x = (senx)/x= cosx/1 = (cos0)/1 = 1/1
mas nao entendi o motivo
Att
G. Feron
obrigado!
-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
 por MarceloFantini » Dom Mai 06, 2012 22:53
por MarceloFantini » Dom Mai 06, 2012 22:53
Este é um dos chamados limites fundamentais, onde
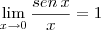
. O importante é perceber que sempre que a variável do seno estiver dividindo-o e ambos tenderem para zero, então o limite é 1.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- T.Confronto
por PeIdInHu » Ter Jul 20, 2010 02:45
- 0 Respostas
- 897 Exibições
- Última mensagem por PeIdInHu

Ter Jul 20, 2010 02:45
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do Confronto
por Claudin » Qua Mai 25, 2011 19:51
- 3 Respostas
- 3437 Exibições
- Última mensagem por LuizAquino

Qua Mai 25, 2011 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do Confronto
por Cleyson007 » Seg Jul 11, 2011 22:02
- 3 Respostas
- 2434 Exibições
- Última mensagem por MarceloFantini

Ter Jul 12, 2011 09:05
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do confronto
por jemourafer » Dom Abr 01, 2012 20:23
- 1 Respostas
- 1674 Exibições
- Última mensagem por NMiguel

Dom Abr 01, 2012 21:00
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES - Teorema do confronto
por paola-carneiro » Dom Jun 03, 2012 20:53
- 1 Respostas
- 1905 Exibições
- Última mensagem por Fabio Wanderley

Seg Jun 04, 2012 02:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
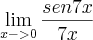


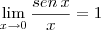 . O importante é perceber que sempre que a variável do seno estiver dividindo-o e ambos tenderem para zero, então o limite é 1.
. O importante é perceber que sempre que a variável do seno estiver dividindo-o e ambos tenderem para zero, então o limite é 1.
