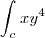[Integrais de linha]

por **AlexandreTS** » Sáb Mai 05, 2012 22:52

Calcular $\int_{c}^{}x{y}^{4}$ , sendo C a metade direita do círculo ${x}^{2} + {y}^{2}$ = 16.

O que eu fiz:
1) Achar uma parametrização x(t) e y(t):
Utilizei x(t) = cos(t) e y(t) = sen(t). Elevando as derivadas das funções componentes ao quadrado, somando elas e colocando na raiz, temos 1, então a integral de linha fica igual a:

$\int_{c}^{}cos(t){sen(t)}^{4}$

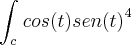
2) Coloquei como limites de integração $\frac{-\pi}{2} e \frac{\pi}{2}$ .

3) Fiz então a substituição u = ${sen(t)}^{2}$ , de modo que dt = $\frac{du}{2cos(t)}$ e a integral fica assim:
$\frac{1}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}{u}^{2}du$
A partir disso ficou fácil calcular o valor da integral, mas o resultado, segundo o livro, é de 1638,4. Não sei em que parte errei, se os limites escolhidos estão certos... tem um momento em que eu elimino o cosseno da integral por uma divisão; acho que isso está errado, mas não sei se foi exatamente nessa parte que eu errei.

Ajudem por favor!

por **AlexandreTS** » Sáb Mai 05, 2012 22:55

Aaaah o que eu errei foi na parametrização, certo? Eu preciso colocar rcos(t) e rsen(t), então teria x(t) = 4cos(t) e y(t) = 4sen(t)... certo?

[Integrais de linha]

[Integrais de linha]

[Integrais de linha]

Re: [Integrais de linha]

Quem está online