 por raimundoocjr » Sex Mai 04, 2012 19:57
por raimundoocjr » Sex Mai 04, 2012 19:57
01. Uma aeronave faz sua aproximação final do destino, quando seu comandante é informado pelo controlador de voo que, devido ao intenso tráfego aéreo, haverá um tempo de espera de 15 minutos para que o pouso seja autorizado e que ele deve permanecer em rota circular, em torno da torre de controle do aeroporto, a 1 500 metros de altitude, até que a autorização para o pouso seja dada. O comandante, cônscio do tempo de espera a ser despendido e de que, nessas condições, a aeronave que pilota voa a uma velocidade constante de

(km/h), decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar. Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.

a)
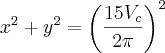
b)
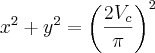
c)
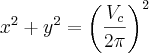
d)
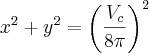
e)
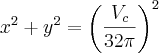
Tentativa de Resolução;
Não estou obtendo resultado satisfatório ao relacionar a velocidade com outros aspectos.
Gabarito: D
-
raimundoocjr
-
 por LuizAquino » Sáb Mai 05, 2012 11:54
por LuizAquino » Sáb Mai 05, 2012 11:54
raimundoocjr escreveu:01. Uma aeronave faz sua aproximação final do destino, quando seu comandante é informado pelo controlador de voo que, devido ao intenso tráfego aéreo, haverá um tempo de espera de 15 minutos para que o pouso seja autorizado e que ele deve permanecer em rota circular, em torno da torre de controle do aeroporto, a 1 500 metros de altitude, até que a autorização para o pouso seja dada. O comandante, cônscio do tempo de espera a ser despendido e de que, nessas condições, a aeronave que pilota voa a uma velocidade constante de

(km/h), decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar. Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.
a)
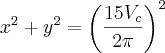
b)
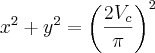
c)
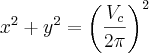
d)
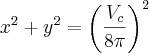
e)
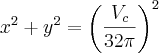
raimundoocjr escreveu:Tentativa de Resolução:
Não estou obtendo resultado satisfatório ao relacionar a velocidade com outros aspectos.
Gabarito: D
Se a velocidade é de Vc km/h, então em 1 hora ele percorre Vc km. Desse modo, em 15 minutos ele irá percorrer (Vc/4) km.
Note que essa distância percorrida será equivalente ao comprimento de uma circunferência (já que ele dará apenas uma volta).
Considerando essas informações, tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- GEOMETRIA ANALITICA. EQUAÇÃO POLAR
por ALEXSANDRO » Qui Mar 29, 2012 16:52
- 5 Respostas
- 3681 Exibições
- Última mensagem por MarceloFantini

Qua Abr 11, 2012 21:10
Geometria Analítica
-
- [Geometria Analitica] Equação de reta
por LucasSG » Qui Jun 06, 2013 22:45
- 1 Respostas
- 2225 Exibições
- Última mensagem por e8group

Sáb Jun 08, 2013 22:15
Geometria Analítica
-
- Geometria Analítica - Equação segmentária
por Flordelis25 » Sex Ago 16, 2013 20:31
- 1 Respostas
- 1645 Exibições
- Última mensagem por MateusL

Sáb Ago 17, 2013 01:48
Geometria Analítica
-
- [Geometria Analítica]Equação da Reta
por IlgssonBraga » Ter Nov 05, 2013 14:34
- 1 Respostas
- 1634 Exibições
- Última mensagem por e8group

Sex Nov 15, 2013 12:25
Geometria Analítica
-
- [Geometria Analítica] Simplificar a equação
por esthinri » Qua Jun 04, 2014 12:59
- 0 Respostas
- 1244 Exibições
- Última mensagem por esthinri

Qua Jun 04, 2014 12:59
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (km/h), decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar. Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.
(km/h), decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar. Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.
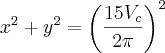
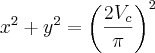
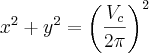
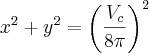
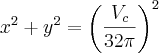




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.