 por Talitafreire » Qui Jul 09, 2009 17:29
por Talitafreire » Qui Jul 09, 2009 17:29
Olá gente. Sou novata e entrei aqui pq tenho uma dúvida em uma questão q caiu numa prova de cálculo q fiz.
Bom, a questão pede para esboçar o gráfico da seguinte função:
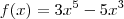
Já consegui encontrar os pontos críticos, concavidades, os intervalos onde a função é crescente e decrescente, o limite quando tende a zero, mas estou com muita dificuldade para encontrar as assíntotas dessa função (se é q elas existem), oq faz com q meu gráfico não saia. :/. Quem puder, ajude-me ok? Obrigada desde já.
-
Talitafreire
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 09, 2009 17:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química (Bacharelado)
- Andamento: cursando
 por Marcampucio » Qui Jul 09, 2009 17:59
por Marcampucio » Qui Jul 09, 2009 17:59
Veja Talita,
o domínio da função é todo o campo Real, portanto ela é contínua e não tem assíntotas verticais.
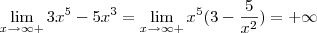
anlogamente

a função não tem assíntotas horizontais também.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Talitafreire » Qui Jul 09, 2009 18:03
por Talitafreire » Qui Jul 09, 2009 18:03
Marcampucio escreveu:Veja Talita,
o domínio da função é todo o campo Real, portanto ela é contínua e não tem assíntotas verticais.
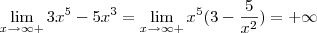
anlogamente

a função não tem assíntotas horizontais também.
Muito obrigada pela resposta ^^ \o/ mesmo mesmo Tentarei montar esse gráfico entao. Até.
-
Talitafreire
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 09, 2009 17:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química (Bacharelado)
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Grafico de limites e assintotas
por Bruhh » Qui Abr 15, 2010 15:43
- 3 Respostas
- 5295 Exibições
- Última mensagem por Marcampucio

Sex Abr 16, 2010 21:07
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Iniciação (Gráfico - assíntotas)
 por ViniciusAlmeida » Seg Fev 09, 2015 12:35
por ViniciusAlmeida » Seg Fev 09, 2015 12:35
- 0 Respostas
- 938 Exibições
- Última mensagem por ViniciusAlmeida

Seg Fev 09, 2015 12:35
Cálculo: Limites, Derivadas e Integrais
-
- Encontrando as raízes!
por gfdbruno » Qui Ago 25, 2011 10:36
- 1 Respostas
- 2526 Exibições
- Última mensagem por gfdbruno

Qui Ago 25, 2011 12:53
Polinômios
-
- assíntotas
 por pseytow » Qua Jul 02, 2008 13:11
por pseytow » Qua Jul 02, 2008 13:11
- 2 Respostas
- 5472 Exibições
- Última mensagem por admin

Sex Jul 04, 2008 05:39
Cálculo: Limites, Derivadas e Integrais
-
- assíntotas
por aquis » Qua Set 10, 2014 11:49
- 0 Respostas
- 1643 Exibições
- Última mensagem por aquis

Qua Set 10, 2014 11:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
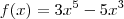




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.