 por LuizCarlos » Sex Mai 04, 2012 12:34
por LuizCarlos » Sex Mai 04, 2012 12:34
Olá amigos professores, estou resolvendo uns exercícios de simplificação de radicais, mas o livro não mostra exemplos de como resolver simplificação de radicais quando envolvem números decimais!
![\sqrt[3]{0,001{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}}](/latexrender/pictures/9dfacc60f746a1d7026d16689437b553.png)
Não estou conseguindo entender, como resolver, esse
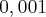
está me causando confusão.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizAquino » Sex Mai 04, 2012 19:02
por LuizAquino » Sex Mai 04, 2012 19:02
LuizCarlos escreveu:Olá amigos professores, estou resolvendo uns exercícios de simplificação de radicais, mas o livro não mostra exemplos de como resolver simplificação de radicais quando envolvem números decimais!
![\sqrt[3]{0,001{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}}](/latexrender/pictures/9dfacc60f746a1d7026d16689437b553.png)
Não estou conseguindo entender, como resolver, esse
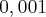
está me causando confusão.
DicaPerceba que 0,001 é equivalente a fração
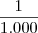
(ou seja, um milésimo). Sendo assim, temos que:
![\sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}}](/latexrender/pictures/e04bbeb0ac237197ed4a589afa58646e.png)
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LuizCarlos » Sex Mai 04, 2012 20:29
por LuizCarlos » Sex Mai 04, 2012 20:29
LuizAquino escreveu:LuizCarlos escreveu:Olá amigos professores, estou resolvendo uns exercícios de simplificação de radicais, mas o livro não mostra exemplos de como resolver simplificação de radicais quando envolvem números decimais!
![\sqrt[3]{0,001{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}}](/latexrender/pictures/9dfacc60f746a1d7026d16689437b553.png)
Não estou conseguindo entender, como resolver, esse
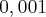
está me causando confusão.
DicaPerceba que 0,001 é equivalente a fração
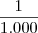
(ou seja, um milésimo). Sendo assim, temos que:
![\sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}}](/latexrender/pictures/e04bbeb0ac237197ed4a589afa58646e.png)
Agora tente terminar o exercício.
Obrigado LuizAquino, consegui entender!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação de radicais
por Andrewo » Sáb Fev 11, 2012 12:06
- 4 Respostas
- 2239 Exibições
- Última mensagem por Andrewo

Seg Fev 13, 2012 15:43
Álgebra Elementar
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2359 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [Simplificação]Fazer a simplificação da resposta
por neoreload » Qua Fev 04, 2015 05:50
- 3 Respostas
- 2878 Exibições
- Última mensagem por neoreload

Sáb Fev 07, 2015 22:10
Equações
-
- [SIMPLIFICAÇÃO] Simplificação expoentes
por brunnkpol » Ter Mai 07, 2013 17:00
- 1 Respostas
- 1835 Exibições
- Última mensagem por DanielFerreira

Sex Mai 10, 2013 00:40
Aritmética
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2341 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{0,001{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}}](/latexrender/pictures/9dfacc60f746a1d7026d16689437b553.png)
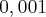 está me causando confusão.
está me causando confusão.
![\sqrt[3]{0,001{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}}](/latexrender/pictures/9dfacc60f746a1d7026d16689437b553.png)
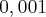 está me causando confusão.
está me causando confusão.
![\sqrt[3]{0,001{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}}](/latexrender/pictures/9dfacc60f746a1d7026d16689437b553.png)
está me causando confusão.
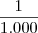 (ou seja, um milésimo). Sendo assim, temos que:
(ou seja, um milésimo). Sendo assim, temos que:![\sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}}](/latexrender/pictures/e04bbeb0ac237197ed4a589afa58646e.png)

![\sqrt[3]{0,001{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}}](/latexrender/pictures/9dfacc60f746a1d7026d16689437b553.png)
está me causando confusão.
(ou seja, um milésimo). Sendo assim, temos que:
![\sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}} \sqrt[3]{0,001{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{1.000}{x}^{3}{y}^{4}} = \sqrt[3]{\frac{1}{10^3}{x}^{3}{y}^{4}}](/latexrender/pictures/e04bbeb0ac237197ed4a589afa58646e.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)