Na aula de Mecânica dos Sólidos o professor resolveu o seguinte exercício:
"Uma estaca cravada no solo( http://imageshack.us/photo/my-images/204/arlan.jpg/) é solicitada por dois trechos de Resultante de Forças Concorrentes corda. Impondo que a resultante das duas forças aplicadas à estaca seja vertical, determine:
a) O valor de alfa para o qual a intensidade de P seja mínima;
b) A correspondente intensidade de P."
Ele resolveu o item a usando a seguinte suposição :"Para que P seja mínima, é necessário que esta seja perpendicular a força de 120N. Com isso chegamos a conclusão que alfa = 65 graus ", e ele mostrou uma animação com Geogebra. Acontece que eu não fiquei conformado com essa resposta e tentei encontra uma uma função usando a lei dos senos e dos cossenos parar em seguida minimiza-la, mas não consegui.
grato desde já


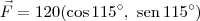

 seja vertical. Para que isso aconteça, devemos ter:
seja vertical. Para que isso aconteça, devemos ter:
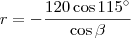
 , basta determinar
, basta determinar  de modo que |r| seja mínimo. Em seguida, note que
de modo que |r| seja mínimo. Em seguida, note que  é o complementar de
é o complementar de 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)