Bem Ai vai: 43 (ITA-SP) Sejam U um conjunto não-vazio e
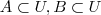 . Usando apenas as definições de igualdade, reunião, intercecção e complementar, prove que:
. Usando apenas as definições de igualdade, reunião, intercecção e complementar, prove que:I- SE
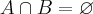 , então
, então 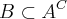 .
.II-SE
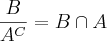 .
.e ai que está , gente eu nem sei como começar. O que o item II ta querendo dizer? e como provar o item I e o II? por favor me ajudem pois eu tentei e não consegui!


PS- essa
 e o complemento do próprio conjunto, eu dei uma pesquisada na net porque eu tabem não sabia hehe. e o item dois tem um divisão do conjunto B pelo complemento do proprio conjunto A ? e isso mesmo? fica a duvida! falow desde já eu agradeço a todos faloww pessoal!
e o complemento do próprio conjunto, eu dei uma pesquisada na net porque eu tabem não sabia hehe. e o item dois tem um divisão do conjunto B pelo complemento do proprio conjunto A ? e isso mesmo? fica a duvida! falow desde já eu agradeço a todos faloww pessoal! 


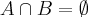 temos que se
temos que se  . (editei aqui p/ corrigir digitação)
. (editei aqui p/ corrigir digitação)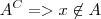 . Assim concluímos que
. Assim concluímos que 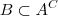 .
.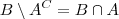 . Aqui
. Aqui 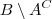 significa
significa  menos
menos 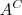 , ou seja o conjunto dos elementos que estão em
, ou seja o conjunto dos elementos que estão em 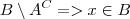 e
e 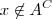 .
. em
em 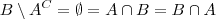 .
.
 só que eu me enganei, como no enunciado diz que
só que eu me enganei, como no enunciado diz que 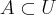 e tambem que
e tambem que 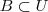 então no
então no 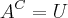 então
então 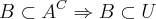 então como
então como 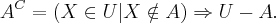 então o que você me falou é verdade que o
então o que você me falou é verdade que o 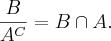 então como
então como 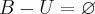 e como a
e como a  ou
ou 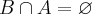 eu entendi que essa igualdade é verdadeira !!!
eu entendi que essa igualdade é verdadeira !!!
 , avisa que eu resolvo.
, avisa que eu resolvo.

