 por maria jose de sousa » Seg Jul 06, 2009 21:53
por maria jose de sousa » Seg Jul 06, 2009 21:53
Estou estudando para passar em concursos, porém ao tentar resolver algumas questões matematicas fui esbarrada nessa:
Q 1. Uma nova penitenciária foi projetada para acomodar 400
detentos em duas alas, sendo que a capacidade da ala maior
corresponde a 5/3 da capacidade da ala menor. A ala maior
foi projetada para acomodar
(A) 150 detentos.
(B) 180 detentos.
(C) 240 detentos.
(D) 250 detentos.(resposta correta pelo gabarito)
(E) 280 detentos.
Q 2. Quatro agentes penitenciários fizeram um determinado número
total de horas extras no último mês. Sabe-se que Luís fez
1/5 desse total, que Mário fez o triplo de Luís, que João fez
1/3 do que Luís fez e que Otávio fez 5 horas extras. Pode-se
concluir, então, que o número de horas extras que Mário fez
nesse mês foi
(A) 2,5.
(B) 7,5.
(C) 15,5.
(D) 22,5.(resposta certa pelo gabarito)
(E) 37,5.
Será que podem me ajudar?...Preciso de uma boa explicação.
-
maria jose de sousa
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jul 06, 2009 21:46
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: administração
- Andamento: formado
 por Marcampucio » Ter Jul 07, 2009 00:49
por Marcampucio » Ter Jul 07, 2009 00:49
A ala menor pode acomodar

detentos e a maior

sendo a soma igual a 400
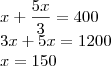
a ala menor acomoda
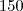
, portanto a maior

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por lucasguedes » Ter Jul 07, 2009 16:20
por lucasguedes » Ter Jul 07, 2009 16:20
Luís = 1/5T
Mário = 3/5T
João = 1/3.1/5T
Otávio = 5
____________________
Luís + Mário + João + Otávio = T ==> 1/5T + 3/5T + 1/15T + 5 = T ==> para igualar as fraçõs vou por tudo sobre 15 então teremos:
3/15T + 9/15T + 1/15T + 5 = T
13/15T + 5 = T
T - 13/15T = 5
2/15T = 5
T = 37,5
Agora é só substituir T por 37,5 então teremos:
Mario = 3/5T ==> Mário = 3/5 . 37,5 = 22,5
Espero ter ajudado!!
-
lucasguedes
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Jun 25, 2009 19:12
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso tecnico em eletrotecnica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- FUNÇÃO NÃO CONSIGO CHEGAR À RESPOSTA CERTA
por DIEGO ALVES LOPES » Sáb Abr 11, 2009 01:53
- 1 Respostas
- 2681 Exibições
- Última mensagem por Molina

Sáb Abr 11, 2009 04:26
Funções
-
- [Função 2º grau] Minha resposta está certa?
por Richard Oliveira » Sex Mai 04, 2012 03:05
- 1 Respostas
- 1721 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 00:06
Funções
-
- não sei como chegar na resposta
por Dankaerte » Seg Ago 31, 2009 17:05
- 3 Respostas
- 5790 Exibições
- Última mensagem por Elcioschin

Seg Ago 31, 2009 23:27
Sistemas de Equações
-
- Porcentagem...(como chegar na resposta?)
por Dyego » Sex Mar 26, 2010 13:45
- 1 Respostas
- 4431 Exibições
- Última mensagem por Dan

Sex Mar 26, 2010 16:31
Matemática Financeira
-
- Como faço para chegar na resposta destas funções?
por Dyego » Sex Mar 26, 2010 02:43
- 2 Respostas
- 1727 Exibições
- Última mensagem por Dyego

Sex Mar 26, 2010 12:03
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 detentos e a maior
detentos e a maior  sendo a soma igual a 400
sendo a soma igual a 400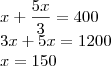
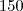 , portanto a maior
, portanto a maior 
