 por nakagumahissao » Qua Abr 04, 2012 20:13
por nakagumahissao » Qua Abr 04, 2012 20:13
Na figura abaixo temos uma sequência de círculos tangentes a duas retas. O raio do primeiro círculo é 1 e o raio do segundo é r < 1. Cada círculo tangencia externamente o círculo anterior. Determine a soma dos raios dos n primeiros círculos.
http://learning.freeiz.com/?p=808Não consegui resolver esta questão de jeito nenhum. Poderiam me auxiliar por favor?
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Guill » Ter Mai 01, 2012 14:57
por Guill » Ter Mai 01, 2012 14:57
Consideremos

os n primeiros raios das circunferências, onde
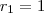
. Se ligarmos o vértice ao centro do outro círculo, teremos uma reta que corta todos os centros das cricunferências (Semelhança de Triângulos).
Se descermos uma reta do centro da primeira circunferência perpendicularmente até o ''chão'', essa reta terá comprimento 1. Façamos o mesmo com todas as circunferências, e tracemos, a partir do centro anterior, uma reta perpendicular ao raio da anterior (o raio que encosta no chão), fechando triângulos retângulos. Pelo teorêma de Pitágoras (para dois raios hipotéticos):


![b=2.\sqrt[]{{r}_{x}.{r}_{x-1}} b=2.\sqrt[]{{r}_{x}.{r}_{x-1}}](/latexrender/pictures/cb9020cf21ae1982858da921e9a72d58.png)
Agora é simples. Basta calcular a soma pelo Teorema de Pitágoras no triângulo maior:
![\left({r}_{1}+{r}_{2}+...+{r}_{n} \right)^2=({r}_{1})^2+\left(2.\sum_{p=1}^{n} \sqrt[]{{r}_{p}.{r}_{p-1}} \right) ^2 \left({r}_{1}+{r}_{2}+...+{r}_{n} \right)^2=({r}_{1})^2+\left(2.\sum_{p=1}^{n} \sqrt[]{{r}_{p}.{r}_{p-1}} \right) ^2](/latexrender/pictures/343b444f6f96f2f7b3212bc1081467f5.png)
[Unparseable or potentially dangerous latex formula. Error 6 ]
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Ter Mai 01, 2012 16:40
por nakagumahissao » Ter Mai 01, 2012 16:40
Muito Obrigado. Assim que eu puder estarei verificando.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- grafico com duas retas tangentes tocando uma circunferencia
 por sonek182 » Qua Ago 19, 2009 17:51
por sonek182 » Qua Ago 19, 2009 17:51
- 0 Respostas
- 1731 Exibições
- Última mensagem por sonek182

Qua Ago 19, 2009 17:51
Trigonometria
-
- Círculos e Retas - Determinar Coordenadas de P ?
por Mateus Pereira » Sex Abr 14, 2017 18:15
- 0 Respostas
- 1421 Exibições
- Última mensagem por Mateus Pereira

Sex Abr 14, 2017 18:15
Geometria Analítica
-
- retas tangentes
por kvothe » Sex Mai 06, 2011 17:48
- 1 Respostas
- 1843 Exibições
- Última mensagem por LuizAquino

Sex Mai 06, 2011 18:49
Cálculo: Limites, Derivadas e Integrais
-
- Retas tangentes à parabola
por Filipe Ricardo Rosa » Dom Jul 03, 2011 19:26
- 8 Respostas
- 9150 Exibições
- Última mensagem por LuizAquino

Qua Jul 06, 2011 10:21
Cálculo: Limites, Derivadas e Integrais
-
- Retas tangentes ao gráfico
por Marcos_Mecatronica » Sáb Abr 27, 2013 19:58
- 1 Respostas
- 1872 Exibições
- Última mensagem por young_jedi

Dom Abr 28, 2013 12:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 os n primeiros raios das circunferências, onde
os n primeiros raios das circunferências, onde 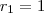 . Se ligarmos o vértice ao centro do outro círculo, teremos uma reta que corta todos os centros das cricunferências (Semelhança de Triângulos).
. Se ligarmos o vértice ao centro do outro círculo, teremos uma reta que corta todos os centros das cricunferências (Semelhança de Triângulos).

![b=2.\sqrt[]{{r}_{x}.{r}_{x-1}} b=2.\sqrt[]{{r}_{x}.{r}_{x-1}}](/latexrender/pictures/cb9020cf21ae1982858da921e9a72d58.png)
![\left({r}_{1}+{r}_{2}+...+{r}_{n} \right)^2=({r}_{1})^2+\left(2.\sum_{p=1}^{n} \sqrt[]{{r}_{p}.{r}_{p-1}} \right) ^2 \left({r}_{1}+{r}_{2}+...+{r}_{n} \right)^2=({r}_{1})^2+\left(2.\sum_{p=1}^{n} \sqrt[]{{r}_{p}.{r}_{p-1}} \right) ^2](/latexrender/pictures/343b444f6f96f2f7b3212bc1081467f5.png)


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.