 por DanielFerreira » Dom Abr 29, 2012 21:06
por DanielFerreira » Dom Abr 29, 2012 21:06
danjr5 escreveu:Calcule
![\int_{}^{}\int_{B}^{}\frac{\sqrt[3]{y - x}}{1 + y + x} \int_{}^{}\int_{B}^{}\frac{\sqrt[3]{y - x}}{1 + y + x}](/latexrender/pictures/06516d1993a243b24558b3ddcf554128.png)
dx dy onde B é o triângulo de vértices
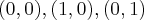
Aplicando Mudança Linear, ficou:
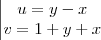
Jacobiano:

Minha integral ficou assim:
![\int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2} \int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2}](/latexrender/pictures/5b01331f1e3c7696a96f0c999b993d8c.png)
du dv
Resultando em
zero.
Poderiam confirmar se o intervalo está correto?
Desde já agradeço.
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizAquino » Ter Mai 01, 2012 15:44
por LuizAquino » Ter Mai 01, 2012 15:44
danjr5 escreveu:danjr5 escreveu:Calcule
![\iint_{B} \frac{\sqrt[3]{y - x}}{1 + y + x} \iint_{B} \frac{\sqrt[3]{y - x}}{1 + y + x}](/latexrender/pictures/cb00d9e3ca29666488b1b6f93fa030e5.png)
dx dy onde B é o triângulo de vértices
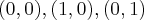
Aplicando Mudança Linear, ficou:
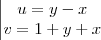
Jacobiano:

Nesse caso o Jacobiano é -1/2.
danjr5 escreveu:Minha integral ficou assim:
![\int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2} \int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2}](/latexrender/pictures/5b01331f1e3c7696a96f0c999b993d8c.png)
du dv
Resultando em
zero.
Poderiam confirmar se o intervalo está correto?
Como B é triângulo de vértices (0, 0), (1, 0) e (0, 1), temos que
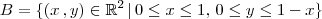
.
Considerando a substituição u = y - x e v = 1 + y + x, temos que:
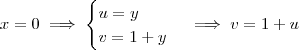
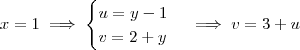


Traçando os gráficos no sistema de eixos uv, temos a figura abaixo.
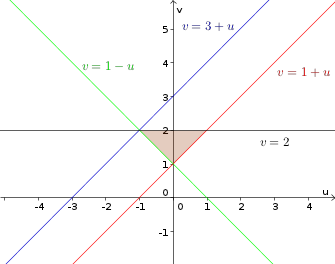
- figura.png (5.04 KiB) Exibido 1850 vezes
Desse modo, temos que:
![\iint_{B} \frac{\sqrt[3]{y - x}}{1 + y + x} \, dx \, dy = \int_{1}^{2}\int_{1-v}^{-1+v} \frac{\sqrt[3]{u}}{2v} \, du \, dv \iint_{B} \frac{\sqrt[3]{y - x}}{1 + y + x} \, dx \, dy = \int_{1}^{2}\int_{1-v}^{-1+v} \frac{\sqrt[3]{u}}{2v} \, du \, dv](/latexrender/pictures/40aa0c1036f063729dd4d3e3cb049ed8.png)
Agora termine o exercício.
Editado pela última vez por
LuizAquino em Ter Mai 01, 2012 15:56, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por DanielFerreira » Ter Mai 01, 2012 15:51
por DanielFerreira » Ter Mai 01, 2012 15:51
LuizAquino,
boa tarde!!
Quanto ao Jacobiano, ouvi o professor dizer que deveríamos usar o módulo. Se puder esclarecer serei grato mais uma vez.
Até breve!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizAquino » Ter Mai 01, 2012 15:56
por LuizAquino » Ter Mai 01, 2012 15:56
danjr5 escreveu: Quanto ao Jacobiano, ouvi o professor dizer que deveríamos usar o módulo. Se puder esclarecer serei grato mais uma vez.
De fato, devemos usar o módulo do Jacobiano quando vamos substituir na integral.
Nesse caso o Jacobiano é -1/2, portanto na integral iremos colocar |-1/2| = 1/2.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mudança de Variável
por DanielFerreira » Dom Abr 22, 2012 13:58
- 2 Respostas
- 1605 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas em mudança de variável
por pam_nivens » Sáb Nov 28, 2009 21:26
- 2 Respostas
- 5457 Exibições
- Última mensagem por pam_nivens

Dom Nov 29, 2009 01:37
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variavel na integral
por matmatco » Ter Abr 23, 2013 22:29
- 0 Respostas
- 1120 Exibições
- Última mensagem por matmatco

Ter Abr 23, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variável em exercício de integração
por Skyliner » Qua Nov 25, 2009 23:02
- 2 Respostas
- 3459 Exibições
- Última mensagem por Skyliner

Qui Nov 26, 2009 01:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Mudança de variável
por VFernandes » Ter Jan 03, 2012 23:47
- 2 Respostas
- 2138 Exibições
- Última mensagem por VFernandes

Qui Jan 05, 2012 23:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
dx dy onde B é o triângulo de vértices
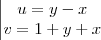

![\int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2} \int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2}](/latexrender/pictures/5b01331f1e3c7696a96f0c999b993d8c.png) du dv
du dv
dx dy onde B é o triângulo de vértices
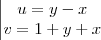

![\int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2} \int_{0}^{1}\int_{v - 1}^{- v + 1}\frac{\sqrt[3]{u}}{v}.\frac{1}{2}](/latexrender/pictures/5b01331f1e3c7696a96f0c999b993d8c.png) du dv
du dv
dx dy onde B é o triângulo de vértices
du dv
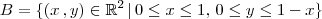 .
.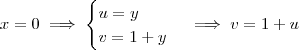
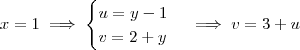


![\iint_{B} \frac{\sqrt[3]{y - x}}{1 + y + x} \, dx \, dy = \int_{1}^{2}\int_{1-v}^{-1+v} \frac{\sqrt[3]{u}}{2v} \, du \, dv \iint_{B} \frac{\sqrt[3]{y - x}}{1 + y + x} \, dx \, dy = \int_{1}^{2}\int_{1-v}^{-1+v} \frac{\sqrt[3]{u}}{2v} \, du \, dv](/latexrender/pictures/40aa0c1036f063729dd4d3e3cb049ed8.png)



