Prezado colega:
Estive revendo sua demonstração e encontrei uma falha nela:
ogojy escreveu:s + x > tg xparas > 0impossivel, um absurdo
Onde s + x > tg x, não é absurdo, mas sim uma verdade incontestável, já que, se s + y > tg x e y = x + n, para um valor n positivo qualquer. Por isso, me sinto na obrigação de criar uma nova demonstração para substituir essa:
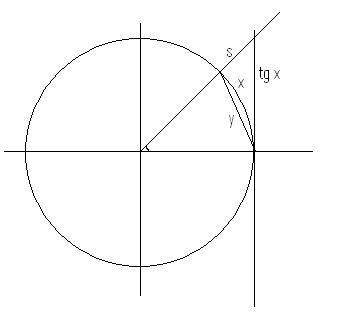
No seu ciclo trigonométrico, temos um triângulo de catetos tg x e 1. Contido nele, temos uma fatia da citcunferência, de ângulo x radianos. Logicamente, a área da fatia é menor que a área do triângulo (em x = 0 essa área é igual):

A área do triângulo é a metade do produto dos catetos, enquato que a área da fatia é metade do comprimeto do arco (por regra de três: Área da circunferência total é

e o comprimento total da mesma é
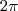
):
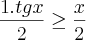

Essa demonstração nos permite ver que essa desigualdade é válida no primeiro quadrante, mas nada garante sobre os demais.




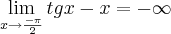


 e o comprimento total da mesma é
e o comprimento total da mesma é 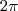 ):
):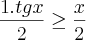

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.