 por andersontricordiano » Seg Dez 05, 2011 21:59
por andersontricordiano » Seg Dez 05, 2011 21:59
Calcule o valor da expressão
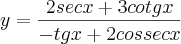
, sendo x um arco do 2º quadrante e cos x=
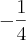
Resposta:
![\frac{-3-8\sqrt[]{15}}{23} \frac{-3-8\sqrt[]{15}}{23}](/latexrender/pictures/667085793ad38982338ae4a6d104436a.png)
Agradeço quem resolver!!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Seg Abr 30, 2012 00:43
por nakagumahissao » Seg Abr 30, 2012 00:43
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Calculo de trigonometria) Calcule o valor de 4cosx/2senx
por andersontricordiano » Seg Ago 08, 2011 16:21
- 1 Respostas
- 1116 Exibições
- Última mensagem por MarceloFantini

Seg Ago 08, 2011 21:50
Trigonometria
-
- (Calculo de trigonometria) Calcule sen x - cos x
por andersontricordiano » Seg Ago 08, 2011 18:45
- 1 Respostas
- 1464 Exibições
- Última mensagem por DanielFerreira

Dom Abr 01, 2012 16:14
Trigonometria
-
- Trigonometria: Cálculo da Expressão Trigonométrica
por leotecco » Qui Mai 21, 2015 19:59
- 0 Respostas
- 1783 Exibições
- Última mensagem por leotecco

Qui Mai 21, 2015 19:59
Trigonometria
-
- (Calculo de trigonometria) Determine o valor de x+10
por andersontricordiano » Ter Dez 06, 2011 14:36
- 1 Respostas
- 1554 Exibições
- Última mensagem por MarceloFantini

Ter Dez 06, 2011 14:54
Trigonometria
-
- [Calcule o valor de Seno de 18º] Expressar o valor numérico
por VictorFPS » Sáb Fev 14, 2015 20:01
- 1 Respostas
- 3856 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:41
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
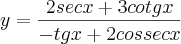 , sendo x um arco do 2º quadrante e cos x=
, sendo x um arco do 2º quadrante e cos x=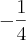
![\frac{-3-8\sqrt[]{15}}{23} \frac{-3-8\sqrt[]{15}}{23}](/latexrender/pictures/667085793ad38982338ae4a6d104436a.png)

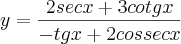 , sendo x um arco do 2º quadrante e cos x=
, sendo x um arco do 2º quadrante e cos x=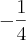
![\frac{-3-8\sqrt[]{15}}{23} \frac{-3-8\sqrt[]{15}}{23}](/latexrender/pictures/667085793ad38982338ae4a6d104436a.png)


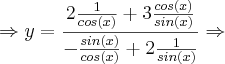

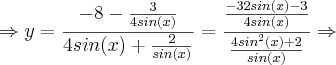
![\Rightarrow y = \frac{-3 -32sin(x)}{16{sin}^{2}(x) + 8} = \frac{-3 -32\sqrt[2]{1 - {cos}^{2}(x)}}{16(1 - {cos}^{2}(x) + 8} \Rightarrow \Rightarrow y = \frac{-3 -32sin(x)}{16{sin}^{2}(x) + 8} = \frac{-3 -32\sqrt[2]{1 - {cos}^{2}(x)}}{16(1 - {cos}^{2}(x) + 8} \Rightarrow](/latexrender/pictures/5ac7232980492c14fff899061ec32d66.png)
![\Rightarrow y = \frac{-3 -32\sqrt[2]{1 - \frac{1}{16}}}{16(1 - \frac{1}{16}) + 8} = \frac{-3 -32\sqrt[2]{\frac{15}{16}} }{16(\frac{15}{16}) + 8} \Rightarrow \Rightarrow y = \frac{-3 -32\sqrt[2]{1 - \frac{1}{16}}}{16(1 - \frac{1}{16}) + 8} = \frac{-3 -32\sqrt[2]{\frac{15}{16}} }{16(\frac{15}{16}) + 8} \Rightarrow](/latexrender/pictures/da49dea4b126bb298b599c94193dbed4.png)
![\Rightarrow y = \frac{-3 - \frac{32}{4}\sqrt[2]{15}}{23} \Rightarrow \Rightarrow y = \frac{-3 - \frac{32}{4}\sqrt[2]{15}}{23} \Rightarrow](/latexrender/pictures/43802a686ff184568ee764d4827a8547.png)
![\Rightarrow y = \frac{-3 - 8 \sqrt[2]{15}}{23} \Rightarrow y = \frac{-3 - 8 \sqrt[2]{15}}{23}](/latexrender/pictures/b00123cca6a808a8c0073b5bedf3279a.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.