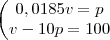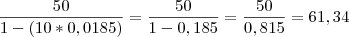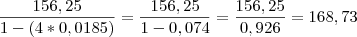por maninhx » Qui Abr 19, 2012 22:31
por maninhx » Qui Abr 19, 2012 22:31
Pessoal, trabalho com desconto de cheques e boletos no banco. O banco me cobra uma taxa de 1,85% ao mês. Tenho uma planilha disponibilizada pelo próprio banco, no qual eu coloco o valor das parcelas, e ela me da o valor líquido que irá me sobrar. Porém digamos que vendi algo no valor de R$1000,00 a vista, e quero receber líquido esses mesmos R$1000,00 e os juros do banco irei cobrar do cliente. Na planilha do banco, tenho que ir ajustando as parcelas, até fechar o valor líquido de R$1000,00. Gostaria de algo mais ágil, gostaria de um cálculo para que a partir do valor líquido eú já saiba quanto terei de cobrar do meu cliente. Já usei várias fórmulas, e sempre da diferença com os valores da planilha.
Tentei anexar a planilha não aceitou a extensão. Se ela foi útilo, eu posto ela num site de upload.
-
maninhx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Abr 19, 2012 21:28
- Formação Escolar: SUPLETIVO
- Área/Curso: Analise e Desenvolvimento de Sistemas
- Andamento: formado
 por Fabiano Vieira » Sáb Abr 28, 2012 21:07
por Fabiano Vieira » Sáb Abr 28, 2012 21:07
Coloque a planilha para a gente ver.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por maninhx » Ter Mai 01, 2012 20:47
por maninhx » Ter Mai 01, 2012 20:47
Não consegui anexar pelo forum então hospedei. Abaixo o link da planilha
http://www.sendspace.com/file/j002gj
-
maninhx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Abr 19, 2012 21:28
- Formação Escolar: SUPLETIVO
- Área/Curso: Analise e Desenvolvimento de Sistemas
- Andamento: formado
 por Fabiano Vieira » Ter Mai 01, 2012 23:33
por Fabiano Vieira » Ter Mai 01, 2012 23:33
Vou colocar um exemplo baseado no que estou entendendo a respeito.
Suponha que você vendeu um produto no valor de R$ 1000,00 para ser pago em 5 meses.
O banco cobra uma taxa de 1,85 ao mês (0,0185), então os juros cobrados pelo banco em 5 meses é
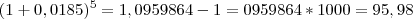
Se for isso, você pode dividir o juros pelo mesmo período( 5 meses), o que ficaria uma mensalidade de, aproximadamente, R$219,20.
Seguindo os mesmos critérios da planilha que você enviou, teria um valor líquido final de R$ 998,40.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por Fabiano Vieira » Qua Mai 02, 2012 22:07
por Fabiano Vieira » Qua Mai 02, 2012 22:07
Deu certo dessa forma ?
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por maninhx » Qui Mai 03, 2012 10:03
por maninhx » Qui Mai 03, 2012 10:03
Ainda não tive tempo para verificar. Farei isso hoje a noite e dou uma resposta. Obrigado
-
maninhx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Abr 19, 2012 21:28
- Formação Escolar: SUPLETIVO
- Área/Curso: Analise e Desenvolvimento de Sistemas
- Andamento: formado
 por maninhx » Qui Mai 03, 2012 21:47
por maninhx » Qui Mai 03, 2012 21:47
Coloquei essas parcelas na planilha, e deu líquido R$1031,17 (sem o IOF).
-
maninhx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Abr 19, 2012 21:28
- Formação Escolar: SUPLETIVO
- Área/Curso: Analise e Desenvolvimento de Sistemas
- Andamento: formado
 por Fabiano Vieira » Dom Mai 06, 2012 01:43
por Fabiano Vieira » Dom Mai 06, 2012 01:43
maninhx escreveu:Coloquei essas parcelas na planilha, e deu líquido R$1031,17 (sem o IOF).
Analisando a planilha, a última parcela seria no começo do quinto mês, e como os juros são contados apenas ao final de cada mês, vamos tentar com um período a menos:
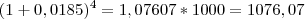
Parcelas:
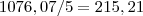
Arredondar para 215,25.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por maninhx » Seg Mai 07, 2012 21:51
por maninhx » Seg Mai 07, 2012 21:51
Fabiano, esse teu cálculo foi o que deu mesno diferença no valor. Porém em 10x deu R$54,00 de diferença. É pouco, mas numa venda faz diferença. Se puder continuar me ajudando eu agradeço.
-
maninhx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Abr 19, 2012 21:28
- Formação Escolar: SUPLETIVO
- Área/Curso: Analise e Desenvolvimento de Sistemas
- Andamento: formado
 por Fabiano Vieira » Qua Mai 09, 2012 00:51
por Fabiano Vieira » Qua Mai 09, 2012 00:51
maninhx,
Através de um sistema de equação, ao que parece, deu para chegar num cálculo correto.
Seguindo o mesmo exemplo dos R$ 1000 em 10 parcelas de R$ 100. Com o sistema fica:
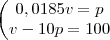
r - 10*0.0185r = 100
r - 0,185r = 100
815r = 100
r = 100/0,815 = 122, 7
(coloque essa parcela na planilha para que tenhamos certeza)Resumindo, a fórmula seria o seguinte:

n = período(meses)
i = taxa(0,0185)
P = parcela sem os juros(nesse caso os R$ 100)
PJ = valor da parcela com juros embutido
Com outros valores...
R$ 500 em 10 parcelas de R$ 50:
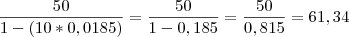
R$ 625 em 4 parcelas de R$ 156,25:
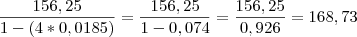
Agora tem que colocar essas parcelas na planilha para confirmar o resultado.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular Valor Bruto a partir do líquido
por AntonioBR » Seg Mai 17, 2010 18:32
- 6 Respostas
- 27123 Exibições
- Última mensagem por Lss

Ter Mar 21, 2017 17:13
Cálculo: Limites, Derivadas e Integrais
-
- valor bruto a partir do valor liquido
por juan cunha » Ter Mai 03, 2016 10:29
- 3 Respostas
- 17793 Exibições
- Última mensagem por nakagumahissao

Sáb Mai 07, 2016 22:51
Matemática Financeira
-
- [Valor de Mercadoria] A partir do valor total de venda
por Gerson Belini » Qua Out 02, 2013 02:17
- 0 Respostas
- 3902 Exibições
- Última mensagem por Gerson Belini

Qua Out 02, 2013 02:17
Matemática Financeira
-
- valor presente líquido
por igor pontes » Sex Fev 24, 2012 21:55
- 0 Respostas
- 2160 Exibições
- Última mensagem por igor pontes

Sex Fev 24, 2012 21:55
Matemática Financeira
-
- Valor presente Liquido
por uroedda » Ter Nov 22, 2016 15:59
- 0 Respostas
- 1980 Exibições
- Última mensagem por uroedda

Ter Nov 22, 2016 15:59
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



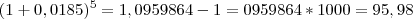
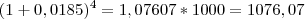
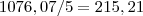 Arredondar para 215,25.
Arredondar para 215,25.