Primeiramente, sabemos que o triângulo ABC é compostro por três lados, AB, BC e AC. Sabemos também que a área de um triângulo é a metade do produto da base pela altura.
Uma vez que temos os pontos médios dos lados como:
M = (0 ; 1 ; 3) ---> Ponto médio de AB
N = (3 ; -2 ; 2) ---> Ponto médio de AC
P = (1 ; 0 ; 2) ---> Ponto médio de BC
Suponhamos os vetores A, B e C tais que:
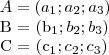
Fica claro que:

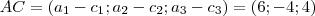

Resolvendo o sistema por igualdade de vetores, encontraremos todos os valores dos vetores. Depois disso, basta calcular o comprimento de cada um dos lados desse triângulo e usar a relação:
![Área = \sqrt[]{p(p-a)(p-b)(p-c)} Área = \sqrt[]{p(p-a)(p-b)(p-c)}](/latexrender/pictures/cc2eaa97c020b4f32cf2f1844f999792.png)
Onde p é o semiperímetro e a, b e c são os lados do triâgulo.


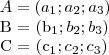

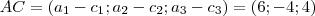

![Área = \sqrt[]{p(p-a)(p-b)(p-c)} Área = \sqrt[]{p(p-a)(p-b)(p-c)}](/latexrender/pictures/cc2eaa97c020b4f32cf2f1844f999792.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.