
- têm casa própria: 38
- têm curso superior: 42
- têm plano de saúde: 70
- têm casa própria e plano de saúde: 34
- têm casa própria e curso superior: 17
- têm curso superior e plano de saúde: 24
- têm casa própria, plano de saúde e curso superior: 15
Qual a porcentagem dos empregados que não se enquadram em nenhuma das situações anteriores? (Sugestão : utilize o diagrama de VENN para facilitar os cálculos)
a) 25%
b) 30%
c) 35%
d) 40%
e) 45%
Cálculo
T
 Número de pessoas entrevistadas.
Número de pessoas entrevistadas.S
 Número de pessoas que disseram sim para pelo menos uma das opções.
Número de pessoas que disseram sim para pelo menos uma das opções.N
 Número de pessoas que disseram não para todas as alternativas.
Número de pessoas que disseram não para todas as alternativas.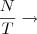 Porcentagem de pessoas que disseram não para todas as alternativas.
Porcentagem de pessoas que disseram não para todas as alternativas.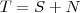
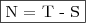

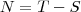

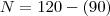

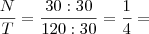 25%
25%R: A
Queria que vocês me informem se esta é a forma correta de se fazer este tipo de exercício, se eu errei ou acertei o exercício e queria que avaliem este exercício de 1 a 10 tendo como base um aluno do 9º ano. Desculpem-me por tantas perguntas!
Desde já agradeço!




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.