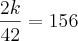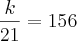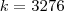por AlexandreLuna » Ter Abr 24, 2012 22:10
por AlexandreLuna » Ter Abr 24, 2012 22:10
2.Certa importância foi distribuída entre quatro pessoas em partes diretamente proporcionais ao número de filhos e inversamente proporcionais ás suas idades. A primeira tem 2 filhos e 42 anos; a segunda , 3 filhos e 50 anos; a terceira 5 filhos e 48 anos e a quarta, 6 filhos e 45 anos. Sabendo-se que a primeira recebeu R$156,00, calcular a importância total e as partes das outras três. Respostas: 1130,61; 196,56; 341,25; 436,80
Este é o tipo de exercício que eu nem sei por onde começar, pois na minha apostila só tem exemplos de exercícios separados em que ou é só proporcional ou é só inversamente proporcional. E não sei qual se faz primeiro se é a idade ou os filhos, e o valor citado da primeira me deixou mais confuso ainda.
-
AlexandreLuna
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 24, 2012 20:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Dom Abr 29, 2012 16:06
por DanielFerreira » Dom Abr 29, 2012 16:06
AlexandreLuna escreveu:2.Certa importância foi distribuída entre quatro pessoas em partes diretamente proporcionais ao número de filhos e inversamente proporcionais ás suas idades. A primeira tem 2 filhos e 42 anos; a segunda , 3 filhos e 50 anos; a terceira 5 filhos e 48 anos e a quarta, 6 filhos e 45 anos. Sabendo-se que a primeira recebeu R$156,00, calcular a importância total e as partes das outras três. Respostas: 1130,61; 196,56; 341,25; 436,80
Este é o tipo de exercício que eu nem sei por onde começar, pois na minha apostila só tem exemplos de exercícios separados em que ou é só proporcional ou é só inversamente proporcional. E não sei qual se faz primeiro se é a idade ou os filhos, e o valor citado da primeira me deixou mais confuso ainda.
Saiba que:
=> se um número é diretamente proporcional a outro, então multiplique; ex: 4 é diretamente proporcional a x, então: 4x
=> se um número é inversamente proporcional a outro, então divida; ex: 4 é inversamente proporcional a x, então:

Imagine que a importância a ser distribuída é k, então:

Foi dito que a 1ª recebeu R$ 156,00,
daí,
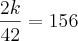
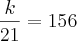
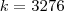
Alexandre,
agora substitua k em cada uma das frações acima e obterá o respectivo valor de cada uma.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão Inversamente proporcional.
por Wizard » Dom Jan 01, 2012 20:27
- 2 Respostas
- 3925 Exibições
- Última mensagem por Wizard

Sex Jan 06, 2012 01:47
Tópicos sem Interação (leia as regras)
-
- Grandeza direta e inversamente proporcional.
por Joseane Lopes » Qua Abr 27, 2011 21:42
- 1 Respostas
- 2509 Exibições
- Última mensagem por MarceloFantini

Qui Abr 28, 2011 00:48
Matemática Financeira
-
- Divisão proporcional
por karenblond » Seg Ago 29, 2011 23:23
- 3 Respostas
- 2683 Exibições
- Última mensagem por Neperiano

Qua Ago 31, 2011 14:58
Sistemas de Equações
-
- DIVISÃO PROPORCIONAL
por Ailton » Ter Fev 21, 2012 01:47
- 0 Respostas
- 1475 Exibições
- Última mensagem por Ailton

Ter Fev 21, 2012 01:47
Matemática Financeira
-
- Divisão Proporcional
por Raphael Feitas10 » Ter Nov 27, 2012 00:25
- 0 Respostas
- 1616 Exibições
- Última mensagem por Raphael Feitas10

Ter Nov 27, 2012 00:25
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.