 por DanielFerreira » Dom Abr 22, 2012 13:58
por DanielFerreira » Dom Abr 22, 2012 13:58
danjr5 escreveu: Calcule
![\int_{D}^{}\int_{}^{}\frac{y + 2x}{\sqrt[]{y - 2x - 1}} \int_{D}^{}\int_{}^{}\frac{y + 2x}{\sqrt[]{y - 2x - 1}}](/latexrender/pictures/4fa5924183f80fb7521ea51dff76916e.png)
dx dy, onde D é a região do plano xy limitada pelas retas y - 2x = 2, y + 2x = 2, y - 2x = 1 e y + 2x = 1
Fiz assim:
considerei...
u = y + 2x
v = y - 2x - 1
Calculei o Jacobiano e encontrei

;
Substituí
u e
v em todas as retas e encontrei: v = 1, u = 2, v = 0 e u =

Minha integral ficou assim:
![\int_{0}^{1}\int_{\frac{1}{2}}^{2}\frac{u}{\sqrt[]{v}}.\frac{1}{4} \int_{0}^{1}\int_{\frac{1}{2}}^{2}\frac{u}{\sqrt[]{v}}.\frac{1}{4}](/latexrender/pictures/4b248b2c804465c7afde02d6d84388fb.png)
du dv
Calculando-a achei
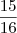
.
Segundo o gabarito é

.
Desde já agradeço a quem puder ajudar.
Att,
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizAquino » Ter Abr 24, 2012 18:48
por LuizAquino » Ter Abr 24, 2012 18:48
danjr5 escreveu: Calcule
![\int_{D}^{}\int_{}^{}\frac{y + 2x}{\sqrt[]{y - 2x - 1}} \int_{D}^{}\int_{}^{}\frac{y + 2x}{\sqrt[]{y - 2x - 1}}](/latexrender/pictures/4fa5924183f80fb7521ea51dff76916e.png)
dx dy, onde D é a região do plano xy limitada pelas retas y - 2x = 2, y + 2x = 2, y - 2x = 1 e y + 2x = 1
Fiz assim:
considerei...
u = y + 2x
v = y - 2x - 1
Calculei o Jacobiano e encontrei

;
Substituí
u e
v em todas as retas e encontrei: v = 1, u = 2, v = 0 e u =

Minha integral ficou assim:
![\int_{0}^{1}\int_{\frac{1}{2}}^{2}\frac{u}{\sqrt[]{v}}.\frac{1}{4} \int_{0}^{1}\int_{\frac{1}{2}}^{2}\frac{u}{\sqrt[]{v}}.\frac{1}{4}](/latexrender/pictures/4b248b2c804465c7afde02d6d84388fb.png)
du dv
Calculando-a achei
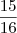
.
Segundo o gabarito é

.
Reveja o intervalo de integração para u. Note que ele será [1, 2].
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por DanielFerreira » Ter Abr 24, 2012 20:31
por DanielFerreira » Ter Abr 24, 2012 20:31
LuizAquino,
muito obrigado. Encontrei o erro!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mudança de Variável
 por DanielFerreira » Dom Abr 29, 2012 21:06
por DanielFerreira » Dom Abr 29, 2012 21:06
- 3 Respostas
- 1866 Exibições
- Última mensagem por LuizAquino

Ter Mai 01, 2012 15:56
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas em mudança de variável
por pam_nivens » Sáb Nov 28, 2009 21:26
- 2 Respostas
- 5453 Exibições
- Última mensagem por pam_nivens

Dom Nov 29, 2009 01:37
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variavel na integral
por matmatco » Ter Abr 23, 2013 22:29
- 0 Respostas
- 1119 Exibições
- Última mensagem por matmatco

Ter Abr 23, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variável em exercício de integração
por Skyliner » Qua Nov 25, 2009 23:02
- 2 Respostas
- 3453 Exibições
- Última mensagem por Skyliner

Qui Nov 26, 2009 01:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Mudança de variável
por VFernandes » Ter Jan 03, 2012 23:47
- 2 Respostas
- 2134 Exibições
- Última mensagem por VFernandes

Qui Jan 05, 2012 23:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
dx dy, onde D é a região do plano xy limitada pelas retas y - 2x = 2, y + 2x = 2, y - 2x = 1 e y + 2x = 1
 ;
;
![\int_{0}^{1}\int_{\frac{1}{2}}^{2}\frac{u}{\sqrt[]{v}}.\frac{1}{4} \int_{0}^{1}\int_{\frac{1}{2}}^{2}\frac{u}{\sqrt[]{v}}.\frac{1}{4}](/latexrender/pictures/4b248b2c804465c7afde02d6d84388fb.png) du dv
du dv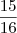 .
. .
.



 .
.



