Um baralho comum de 52 cartas, das quais 12 são figuras (valete, dama e rei), é subdividido aleatoriamente em 3 partes. As partes são colocadas sobre uma mesa com as faces das cartas viradas para baixo. A carta de cima de cada das 3 partes é desvirada. Com base na situação descrita, julgue os itens abaixo.
1) A chance de que as 3 cartas desviradas sejam figuras é maior do que 1%.
Fiz assim: 12/52 x 11/51 x 10/50 => 0,23 X 0,22 x 0,2 => 0,01012 => 1,01% certo , mas no gabarito consta errado.
2) A probabilidade de que exatamente 2 das cartas desviradas sejam figuras está entre 0,08 e 0,13%
Resolução: 12/52 x 11/51 => 0,0506 x 0,8 (40/50) => 0,040 errado, mas no gabarito consta certo.
3) A probabilidade de que pelo menos uma das 3 cartas desviradas seja uma figura é maior do que 0,5%.
=> 0,0506 X 0,8 x 0,79 => 0,032 errada, mas é verdadeira.
De modo geral, questões de probabilidade com baralhos são mais simples, mas não estou conseguindo encontrar o cálculo correto - poderiam ajudar?
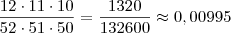
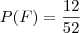
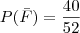
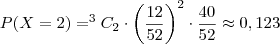(12,3%)
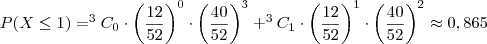(86,5%)
. Ou seja:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.