 por Anniemf » Qua Mar 28, 2012 14:33
por Anniemf » Qua Mar 28, 2012 14:33
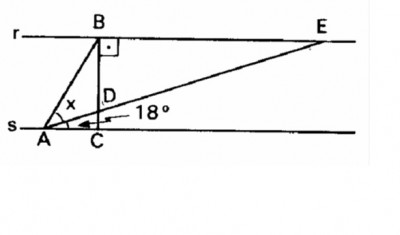
As retas r e s são paralelas e DE=2AB.Calcule x
O que consegui perceber no exercício:
O ângulo BÊD é alterno interno do ângulo DÂF,logo o mesmo vale 18º.
Uma vez que a soma dos ângulos internos do triângulo vale 180º,B^DE=72º
A^DF=72º,pois é oposto pelo vértice do ângulo B^DE
B^DA=108º,pois é suplementar ao ângulo de 72º
- Anexos
-
-
Anniemf
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Mar 28, 2012 14:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por kelvinJhonson » Sáb Abr 21, 2012 23:20
por kelvinJhonson » Sáb Abr 21, 2012 23:20
Oi! Acho que Consegui uma solução tava procurando umas questões pra fazer e acabei vendo essa dai ai vai minha opnião quanto a ela ^^
Afim de facilitar seu raciocínio seja BE=k ; seja AB=w então CD=2w ja que AB=2CD,e seja BD=y.
1º - Observe que existe as seguintes relações no triangulo DBE,
(2w)²+y²=k² ( ' ) e também veja que já que r//s temos que o angulo DÊB = 18 (Ângulos Alternos internos são iguais ^^) então tbm podemos tirar que;Cos 18º =k/2w( '' )
Então Substitua ( '' ) em ( ' )e veja que 4w²+y²= (Cos 18º.2w)² ,então y²=cos 18º.4w²-4w² -> y²= 4w²(1-cos²18º) ->já que (1-cos²18=sen²18) -> y=2w.sen 18 (Tirando a Raiz de ambos os membros afim de achar apenas y em função de w temos que ; y = 2w.sen²18 .
2ºcerto agora é a parte que você se pergunta pra que que eu quero esse y? simples veja que o ângulo x que agente quer está num triangulo que tem nossa querido x e um angulo de 108º como vc observou então use bem ai a Lei Dos Senos para X e 108º então teremos que
y/sen X = w /sen 108º -> 2w sen 18º/sen X = w/sen 108º -> 2.sen 18.sen 108º= sen x (1)
3ºcerto agora observe que sen 108º = sen (90º+18º) (pela formula da soma de dois angulos tiramos dai que) -> sen (90+18) = sen 90º . cos 18º+ sen 18º cos 90º -> como os de 90 agente ja sabe que é cos 90 = 0 e sen 90 = 1 substituindo então sen(90+18)=1.cos18º+sen 18º.0 = cos 18º substituindo em (1) temos que
sen X = 2.sen 18º.cos 18º mais veja tbm que pela formula trigométrica que diz que (2.sen a.cos a = sen 2a) Substituindo temos que sen x = sen (2.18) = sen 36
então X = 36
Espero que tenha Gostado pq eu adorei '-' auhauha xD
-
kelvinJhonson
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 21, 2012 22:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria plana relacionada ao seno]
 por matII » Seg Abr 30, 2012 09:12
por matII » Seg Abr 30, 2012 09:12
- 1 Respostas
- 1326 Exibições
- Última mensagem por Edu-sjc

Seg Abr 30, 2012 14:11
Geometria Plana
-
- Geometria plana pontos notáveis
por matematicodabaixada » Dom Mar 17, 2013 05:41
- 0 Respostas
- 1382 Exibições
- Última mensagem por matematicodabaixada

Dom Mar 17, 2013 05:41
Geometria Plana
-
- Geometria Plana (soma dos 4 angulos)
 por Rafael Pitzer » Seg Fev 11, 2013 18:54
por Rafael Pitzer » Seg Fev 11, 2013 18:54
- 4 Respostas
- 2043 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 17:02
Geometria Plana
-
- Cálculo de ângulos não-notáveis
por Francine » Seg Jun 11, 2012 18:05
- 1 Respostas
- 4229 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 18:35
Trigonometria
-
- Geometria Plana - Questão
por Livia000 » Qui Jun 21, 2012 18:04
- 3 Respostas
- 3524 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 22:26
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
