1. Leis de De Morgan - Dados dois conjuntos A e B, mostre que:
(a) (AUB)^C = A^C?B^C
(b) (A?B)^C = A^C U B^C
Hannibal escreveu:Eu nao estou conseguindo entender bem, essa lei, eu vi pelos diagramas, mais tenho que provar nao so por diagramas mais por elementos, nao estou pedindo resposta mais sim onde procuro?
Bem, tipicamente você encontra esse conteúdo em livros sobre Álgebra de Conjuntos ou ainda sobre Matemática Discreta.
De qualquer modo, você já deve saber que para provar que dois conjuntos são iguais nós temos uma estratégia padrão para isso. Por exemplo, se desejamos provar que X = Y, nós temos que provar duas coisas: 1) se

, então

; 2) se
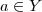
, então

. Ao provar essas duas proposições, no fundo nós provamos que

e

. Quando isso acontece, temos que X = Y.
Por exemplo, considere o quesito (a). Nós temos os conjuntos
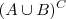
e

. Para provar que eles são iguais, você precisa provar que: 1) se

, então
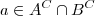
; 2) se

, então
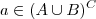
.
Agora tente concluir o exercício.


 , então
, então  ; 2) se
; 2) se 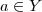 , então
, então  . Ao provar essas duas proposições, no fundo nós provamos que
. Ao provar essas duas proposições, no fundo nós provamos que  e
e  . Quando isso acontece, temos que X = Y.
. Quando isso acontece, temos que X = Y.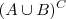 e
e  . Para provar que eles são iguais, você precisa provar que: 1) se
. Para provar que eles são iguais, você precisa provar que: 1) se  , então
, então 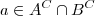 ; 2) se
; 2) se  , então
, então 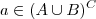 .
.

 .
.
 :
: