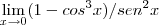 ? O resultado dá 3/2, mas minhas tentativas não deram este valor.
? O resultado dá 3/2, mas minhas tentativas não deram este valor.

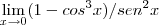 ? O resultado dá 3/2, mas minhas tentativas não deram este valor.
? O resultado dá 3/2, mas minhas tentativas não deram este valor.
Toketsu escreveu:Como se calcula este limite:? O resultado dá 3/2, mas minhas tentativas não deram este valor.

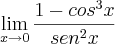
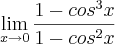
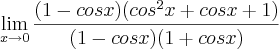
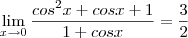

Guill escreveu:
Podemos transformar a equação:
Agora, basta usar o produto notável:

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

