![a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3) a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3)](/latexrender/pictures/f603eb4d5f036bf84aaaaecea4c93ea9.png)
a resposta é a letra d) só que eu quero saber como que resolve por favor?

![a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3) a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3)](/latexrender/pictures/f603eb4d5f036bf84aaaaecea4c93ea9.png)

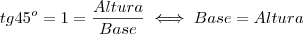
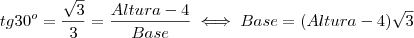
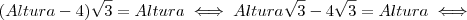
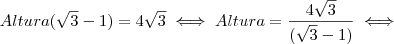
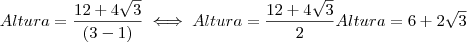
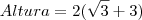

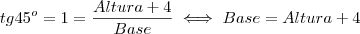
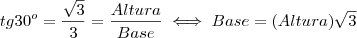
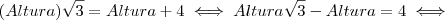
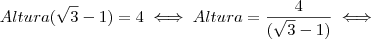
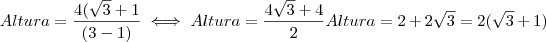


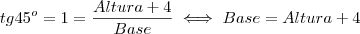
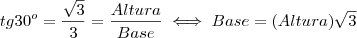
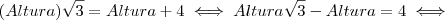
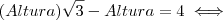 , agora colocaremos Altura em evidência
, agora colocaremos Altura em evidência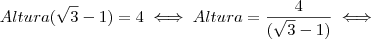 , aqui levamos
, aqui levamos 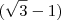 para o segundo membro com a operação inversa .
para o segundo membro com a operação inversa .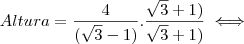 com esta multiplicação obtemos uma diferença de quadrados no denominador que tem como resultado o quadrado do primeiro termo menos o quadrado do segundo termo, assim:
com esta multiplicação obtemos uma diferença de quadrados no denominador que tem como resultado o quadrado do primeiro termo menos o quadrado do segundo termo, assim: 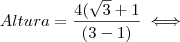
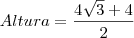 , neste passo efetuamos a multiplicação no numerador e a diferença no denominador.
, neste passo efetuamos a multiplicação no numerador e a diferença no denominador.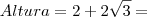 , aqui dividimos por 2 e
, aqui dividimos por 2 e 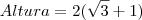 .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.