Dados A (5,2) e B (4,-1), vértices consecutivos de um quadrado, determine os outros dois vértices.
Bom, tentei fazer assim: vértice C (x,y) e vértice D (z,w). Como é um quadrado (lados iguais), então AB = AC = CD = DB sendo as distâncias entre os pontos A ao ponto B e por aí vai, pois é um quadrado. pelas distâncias dos pontos A a B vi que o quadrado tem lado
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) e portnato a diagonal vale 2. Sendo assim tentei encontrar relações entre os pontos A (5,2) e C (x,y) sabendo que o comprimento =
e portnato a diagonal vale 2. Sendo assim tentei encontrar relações entre os pontos A (5,2) e C (x,y) sabendo que o comprimento = ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) e também apelei pra diagonal... mas eu não cheguei a lugar algum! fiz e refiz mas não encontro solução. Quem puder dar uma luz, agradeço desde já!
e também apelei pra diagonal... mas eu não cheguei a lugar algum! fiz e refiz mas não encontro solução. Quem puder dar uma luz, agradeço desde já!

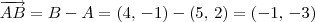
 é ortogonal a
é ortogonal a  (já que ABCD é um quadrado).
(já que ABCD é um quadrado).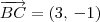 ou
ou 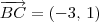 (note que em ambos os casos temos
(note que em ambos os casos temos 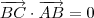 ).
). (já que ABCD é um quadrado).
(já que ABCD é um quadrado).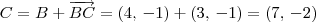
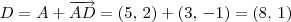
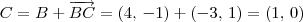
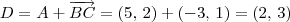

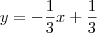 ;
;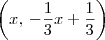 . Além disso, lembre-se que você irá encontrar dois pontos: P = (1, 0) ou P = (7, -2);
. Além disso, lembre-se que você irá encontrar dois pontos: P = (1, 0) ou P = (7, -2);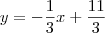 ;
;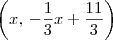 . Além disso, lembre-se que você irá encontrar dois pontos: Q = (8, 1) ou Q = (2, 3).
. Além disso, lembre-se que você irá encontrar dois pontos: Q = (8, 1) ou Q = (2, 3).