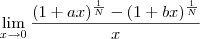
sei que o resultado é
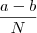 por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa respostagrato pela atenção

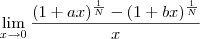
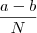 por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
Henrique Bueno escreveu:O limite dado é o seguinte:
sei que o resultado épor recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
![\lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} \lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x}](/latexrender/pictures/8089df1001a4db6fdb55a36f3eceedfc.png)
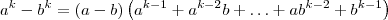
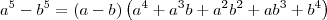
![\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right) \left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)](/latexrender/pictures/e1fb8084d601df16524cb16ab1ad2637.png)
![\left(\sqrt[N]{1 + ax} - \sqrt[N]{1 + bx}\right)\, \left(\sqrt[N]{1 + ax} - \sqrt[N]{1 + bx}\right)\,](/latexrender/pictures/552e312ff2e0a5ae908d9841c979179b.png)
![\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)= \left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)=](/latexrender/pictures/390ddf08c41a798da80585ad12e505ab.png)
![= \left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N = (1 + ax) - (1 + bx) = (a-b)x = \left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N = (1 + ax) - (1 + bx) = (a-b)x](/latexrender/pictures/60a50dee1b548f77b28609509c67ea05.png)
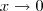 , temos que
, temos que 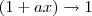 e
e 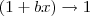 .
.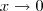 temos que aquela expressão que nós multiplicamos será igual a:
temos que aquela expressão que nós multiplicamos será igual a:![\left(\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}\right) = \left(\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}\right) =](/latexrender/pictures/cf648cff8cb7516734f2a3fe1aa6ce8c.png)

![\lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} = \lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} =](/latexrender/pictures/90075713736f7cabb3c62894c994134e.png)
![= \lim_{x\to 0} \dfrac{\left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)} = \lim_{x\to 0} \dfrac{\left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)}](/latexrender/pictures/d88f2338bc3931bc9c0f9c0da8e048c7.png)
![= \lim_{x\to 0} \dfrac{(a-b)x}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)} = \lim_{x\to 0} \dfrac{(a-b)x}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)}](/latexrender/pictures/d15ea6e2a45881140c5a5064c0b75e9f.png)
![= \lim_{x\to 0} \dfrac{a-b}{\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}} = \lim_{x\to 0} \dfrac{a-b}{\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}}](/latexrender/pictures/ca119c2256a946aa5d175afdcccd55a5.png)
![= \dfrac{a-b}{\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}} = \dfrac{a-b}{\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}}](/latexrender/pictures/a7b0d2dc63b5d2d3250b45b5506c3d93.png)


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)