a)
![4+\sqrt[]{4+2d} 4+\sqrt[]{4+2d}](/latexrender/pictures/b0c4216d5d5edb0c4c2be99efa534a9a.png)
b)
![4+\sqrt[]{2+4d} 4+\sqrt[]{2+4d}](/latexrender/pictures/0af9aad160efb17180f594a48f138484.png)
c)
![2+\sqrt[]{4+2d} 2+\sqrt[]{4+2d}](/latexrender/pictures/2153d70242ce87a5ac8030536738c63b.png)
d)
![2+\sqrt[]{2+4d} 2+\sqrt[]{2+4d}](/latexrender/pictures/50a6850379117209178f6195128ef0b1.png)
Por favor, ajuda!!!

![4+\sqrt[]{4+2d} 4+\sqrt[]{4+2d}](/latexrender/pictures/b0c4216d5d5edb0c4c2be99efa534a9a.png)
![4+\sqrt[]{2+4d} 4+\sqrt[]{2+4d}](/latexrender/pictures/0af9aad160efb17180f594a48f138484.png)
![2+\sqrt[]{4+2d} 2+\sqrt[]{4+2d}](/latexrender/pictures/2153d70242ce87a5ac8030536738c63b.png)
![2+\sqrt[]{2+4d} 2+\sqrt[]{2+4d}](/latexrender/pictures/50a6850379117209178f6195128ef0b1.png)

Pri Ferreira escreveu:Um polígono rgular cum um número par de lados possui d diagonais, que não passam pelo centro da circunferência que o circunscreve. Esse poligono possui o seguinde número de lados.
a)
b)
c)
d)
 .
.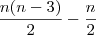 diagonais não passam pelo centro.
diagonais não passam pelo centro.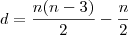

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante