 por emsbp » Qui Abr 12, 2012 18:14
por emsbp » Qui Abr 12, 2012 18:14
Boa tarde.
O enunciado é o seguinte: determine a solução do seguinte problema de valor inicial :
![[cos(ln(2y-8))+\frac{1}{x}]dx +\frac{senx}{y-4}dy=0 [cos(ln(2y-8))+\frac{1}{x}]dx +\frac{senx}{y-4}dy=0](/latexrender/pictures/7cac7a88acdd64dcd7c73c2c372a5b77.png)
; y(1)= 9/2.
Primeiramente, teremos que provar que é uma equação diferencial exata?
Fiz assim, e segundo os meus cálculos ela não é exata:
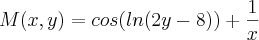
e
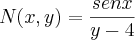
.
Ora,
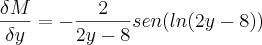
e
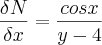
.
Se não me falha nenhum passo, podemos concluir que não é exata.
Estarei a seguir o caminho correto?
Obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Problemas de Valor Inicial] Equações Diferenciais
por mayconf » Ter Abr 15, 2014 18:24
- 1 Respostas
- 2113 Exibições
- Última mensagem por Russman

Ter Abr 15, 2014 22:28
Equações
-
- [Equação diferencial] Problema de valor inicial
por Aliocha Karamazov » Qua Fev 15, 2012 23:34
- 2 Respostas
- 1793 Exibições
- Última mensagem por Aliocha Karamazov

Qui Fev 23, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- (calculo III) resolva o seguinte problema de valor inicial
 por liviabgomes » Qui Dez 01, 2011 14:59
por liviabgomes » Qui Dez 01, 2011 14:59
- 4 Respostas
- 2358 Exibições
- Última mensagem por liviabgomes

Seg Dez 05, 2011 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Integrais (problemas de valor inicial)
por Anne2011 » Sex Set 16, 2011 16:26
- 4 Respostas
- 2357 Exibições
- Última mensagem por Anne2011

Sex Set 16, 2011 18:53
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais
por tiagofabre » Sex Set 21, 2012 00:48
- 1 Respostas
- 1860 Exibições
- Última mensagem por MarceloFantini

Sex Set 21, 2012 01:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[cos(ln(2y-8))+\frac{1}{x}]dx +\frac{senx}{y-4}dy=0 [cos(ln(2y-8))+\frac{1}{x}]dx +\frac{senx}{y-4}dy=0](/latexrender/pictures/7cac7a88acdd64dcd7c73c2c372a5b77.png) ; y(1)= 9/2.
; y(1)= 9/2.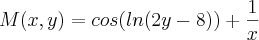 e
e 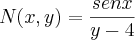 .
.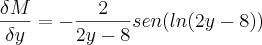 e
e 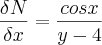 .
.


 .
.



