 por Piva » Qua Abr 11, 2012 15:10
por Piva » Qua Abr 11, 2012 15:10
Boa tarde a todos,
Estou com um pequeno problema em Cálculo numérico. Estou com um programa que rodo no force para a função do SENO. Só que estou com dificuldades para passá-la para COSSENO. Sou iniciante em cálculo numérico, se alguém puder me explicar como eu mudo para o COSSENO eu agradeceria. Eu ja entendi todo o funcionamento do código, porém estou errando em trocar a função.
Segue abaixo o código.
c #############################################################
c Este programa calcula o erro percentual da Serie de Taylor da
c funcaoo sen(bx), expandida no ponto x0
implicit double precision(a-h,o-z)
dimension a(50)
open(5,file='taylor01.1',status='old')
open(6,file='taylor200510.2',status='unknown')
c Ponto de expansao da s‚rie
read(5,*)x0
c Grau da s‚rie polinomial + 1
read(5,*)n_termos
c Coeficiente multiplicador do angulo x
read(5,*)b
c Numero de abscissas
read(5,*)n_x
c Impressao do cabecalho
write(6,5)
c determinacao dos coeficientes da serie de Taylor
do n=1,n_termos
i=1
if(mod(n-1,2).eq.0) then !par
j=1
k=0
if(mod(n-1,4).eq.0) then !múltiplo de 4
i=2
endif
else !ímpar
j=0
k=1
if(mod((n-2),4).eq.0) then !múltiplo de 4 + 1
i=2
endif
endif
a(n)=(-1.d0)**i*b**(n-1)*sin(b*x0)**j*cos(b*x0)**k
enddo
do icont=1,n_x
c Leitura das abscissas em arquivo
read(5,*) x
fxt=0.d0
do n=1,n_termos
c solucao num‚rica
fxt=fxt+a(n)*(x-x0)**(n-1)/fat(n-1)
enddo
c solução analítica
fxa=sin(b*x)
c erro percentual
if(fxa.ne.0.d0) then
erro_p=abs((fxt-fxa)/fxa)*100.d0
write(6,15)x,fxa,fxt,erro_p
else
write(6,20)x,fxa,fxt
endif
enddo
5 format(14x,'x',26x,'f(x)',23x,'F(x)',23x,'E(%)')
15 format(3(f25.14,2x),e25.15)
20 format(3(f25.14,2x),' - ')
stop " Fim "
end
c ##############################################################
function fat(n)
implicit double precision(a-h,o-z)
integer n
fat=dfloat(n)
do i=n,2,-1
xi=dfloat(i)
fat=fat*(xi-1.d0)
enddo
if(n.eq.0) fat=1.d0
return
end
c ##############################################################
Creio que o que tenho que mudar está nessa linha:
a(n)=(-1.d0)**i*b**(n-1)*sin(b*x0)**j*cos(b*x0)**k
Entendo pouco de série de Taylor, mas se me explicarem alguma coisa eu acho que entendo!
Desde já, Obrigado pela ajuda!
-
Piva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jun 29, 2011 18:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 11:58
por LuizAquino » Qui Abr 12, 2012 11:58
Piva escreveu:Boa tarde a todos,
Estou com um pequeno problema em Cálculo numérico. Estou com um programa que rodo no force para a função do SENO. Só que estou com dificuldades para passá-la para COSSENO. Sou iniciante em cálculo numérico, se alguém puder me explicar como eu mudo para o COSSENO eu agradeceria. Eu ja entendi todo o funcionamento do código, porém estou errando em trocar a função.
Segue abaixo o código.
c #############################################################
c Este programa calcula o erro percentual da Serie de Taylor da
c funcaoo sen(bx), expandida no ponto x0
implicit double precision(a-h,o-z)
dimension a(50)
open(5,file='taylor01.1',status='old')
open(6,file='taylor200510.2',status='unknown')
c Ponto de expansao da s‚rie
read(5,*)x0
c Grau da s‚rie polinomial + 1
read(5,*)n_termos
c Coeficiente multiplicador do angulo x
read(5,*)b
c Numero de abscissas
read(5,*)n_x
c Impressao do cabecalho
write(6,5)
c determinacao dos coeficientes da serie de Taylor
do n=1,n_termos
i=1
if(mod(n-1,2).eq.0) then !par
j=1
k=0
if(mod(n-1,4).eq.0) then !múltiplo de 4
i=2
endif
else !ímpar
j=0
k=1
if(mod((n-2),4).eq.0) then !múltiplo de 4 + 1
i=2
endif
endif
a(n)=(-1.d0)**i*b**(n-1)*sin(b*x0)**j*cos(b*x0)**k
enddo
do icont=1,n_x
c Leitura das abscissas em arquivo
read(5,*) x
fxt=0.d0
do n=1,n_termos
c solucao num‚rica
fxt=fxt+a(n)*(x-x0)**(n-1)/fat(n-1)
enddo
c solução analítica
fxa=sin(b*x)
c erro percentual
if(fxa.ne.0.d0) then
erro_p=abs((fxt-fxa)/fxa)*100.d0
write(6,15)x,fxa,fxt,erro_p
else
write(6,20)x,fxa,fxt
endif
enddo
5 format(14x,'x',26x,'f(x)',23x,'F(x)',23x,'E(%)')
15 format(3(f25.14,2x),e25.15)
20 format(3(f25.14,2x),' - ')
stop " Fim "
end
c ##############################################################
function fat(n)
implicit double precision(a-h,o-z)
integer n
fat=dfloat(n)
do i=n,2,-1
xi=dfloat(i)
fat=fat*(xi-1.d0)
enddo
if(n.eq.0) fat=1.d0
return
end
c ##############################################################
Creio que o que tenho que mudar está nessa linha:
a(n)=(-1.d0)**i*b**(n-1)*sin(b*x0)**j*cos(b*x0)**k
Piva escreveu:Entendo pouco de série de Taylor, mas se me explicarem alguma coisa eu acho que entendo!
Esse é o verdadeiro problema: você não sabe expandir (usando a Série de Taylor) a função
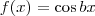
em torno de x0.
Você precisa primeiro saber fazer essa expansão antes de querer mexer no código. Ou seja, você precisa primeiro estudar sobre a Série de Taylor.
Há um vasto material disponível na internet sobre essa assunto. Eu recomendo que você faça uma pesquisa sobre ele.
Vamos então considerar uma função f que possa ser expandida em Série de Taylor. A sua aproximação em torno de x0 será dada por:

Nesse caso, a expansão foi feita até o termo na posição n. Note que você precisa calcular a derivada de f até a ordem n.
Por exemplo, no caso de
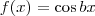
, temos que:

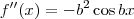


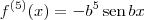
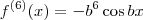
(...)
Agora tente determinar o formato geral. Isto é, o formato para
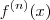
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calculo numerico
por ehrefundini » Qua Mai 07, 2008 10:31
- 1 Respostas
- 2092 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 11:02
Pedidos de Materiais
-
- Calculo Numerico !!
por laisgomes2107 » Sex Set 19, 2008 01:06
- 2 Respostas
- 2937 Exibições
- Última mensagem por admin

Ter Set 23, 2008 18:35
Dúvidas Pendentes (aguardando novos colaboradores)
-
- calculo numerico
por ehrefundini » Sex Mar 06, 2009 10:36
- 1 Respostas
- 2682 Exibições
- Última mensagem por Molina

Sex Mar 06, 2009 13:10
Cálculo Numérico e Aplicações
-
- CALCULO NUMÉRICO I
por futuro fisico » Ter Set 27, 2011 21:04
- 1 Respostas
- 1741 Exibições
- Última mensagem por LuizAquino

Ter Set 27, 2011 22:05
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo numérico
por Jhennyfer » Dom Mai 19, 2013 13:43
- 10 Respostas
- 5109 Exibições
- Última mensagem por Jhennyfer

Dom Mai 19, 2013 16:45
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


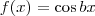 em torno de x0.
em torno de x0.

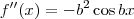


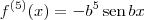
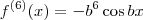
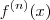 .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.