Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por joaofonseca » Ter Abr 10, 2012 18:35
por joaofonseca » Ter Abr 10, 2012 18:35
Num saco existem n bolas numeradas. Metade têm um número negativo e a outra metade têm um número positivo.
Retiram-se ao acaso duas bolas sem reposição.
Sejam dois acontecimentos:
A-"o produto dos dois números é positivo"
B-"o produto dos dois números é negativo"
Qual dos acontecimentos tem maior probabilidade de se verificar?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por fraol » Ter Abr 10, 2012 20:28
por fraol » Ter Abr 10, 2012 20:28
Veja se você concorda com o raciocínio a seguir:
As probabilidades, caso a caso, são:
Pos = Neg e Neg =>
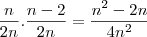
Pos = Pos e Pos =>
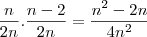
Neg = Neg e Pos =>
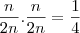
Neg = Pos e Neg =>
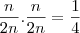
Positivo: A soma dos primeiros 2 casos é a soma de duas parcelas menores que 1/4 que é menor que 50%.
Negativo: A soma dos últimos 2 casos é igual a 50%. Assim o evento B tem maior probabilidade de ocorrer.
Ok?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por joaofonseca » Qua Abr 11, 2012 05:58
por joaofonseca » Qua Abr 11, 2012 05:58
A minha abordagem foi:
Casos possíveis:
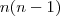
, pois a cada uma das
n bolas pode-se associar uma das restantes.
Acontecimento
A:
Casos favoráveis:
Pos x Pos:
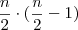
Neg x Neg:
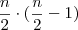
Logo:
![2 \cdot \left[\frac{n}{2} \cdot (\frac{n}{2}-1)\right]=n \cdot (\frac{n}{2}-1)=\frac{n^2}{2}-n=\frac{n^2-2n}{2} 2 \cdot \left[\frac{n}{2} \cdot (\frac{n}{2}-1)\right]=n \cdot (\frac{n}{2}-1)=\frac{n^2}{2}-n=\frac{n^2-2n}{2}](/latexrender/pictures/70b6c77f8dd245696029b26d50bb88db.png)
A probabilidade é:
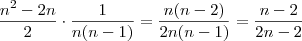
Para o acontecimento
B:
Casos favoráveis:
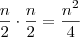
A probabilidade é:
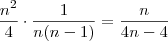
Calculando o limite quando
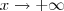
de ambas expressões cheguei a

para o acontecimento
A e

para o acontecimento
B.
Algo deve estar errado no meu raciocínio.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por fraol » Qua Abr 11, 2012 11:24
por fraol » Qua Abr 11, 2012 11:24
Bom dia João,
O meu raciocínio tem um furo ( no total de casos considerados ).
Mais tarde vou revisar e posto a correção.
Também vou analisar a sua resposta.
Grato.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Qua Abr 11, 2012 14:42
por fraol » Qua Abr 11, 2012 14:42
João,
Ao considerar corretamente o total de casos na retirada da segunda bola, as minhas contas ficam iguais às suas, exceto, no caso B, em:
joaofonseca escreveu: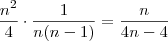
Nesse caso, ao meu ver, é necessário considerar a situação NEG e POS e a POS e NEG, logo devemos multiplicar por 2 o seu resultado que ficaria:
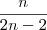
Assim ficamos com:
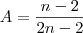
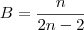
O que dá B > A; pois B > A, se B - A é um número positivo.
(João, o seu desenvolvimento da solução é bastante didático, muito bom.)
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por joaofonseca » Qua Abr 11, 2012 17:06
por joaofonseca » Qua Abr 11, 2012 17:06
Realmente é coenrente que a ordem conte na contabilização dos casos favoráveis ao acontecimento B, já que a contabilização dos casos possíveis também levou em conta a ordem.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por fraol » Qua Abr 11, 2012 17:20
por fraol » Qua Abr 11, 2012 17:20
joaofonseca escreveu:Realmente é coenrente que a ordem conte na contabilização dos casos favoráveis ao acontecimento B, já que a contabilização dos casos possíveis também levou em conta a ordem.
Sim.
Também é coerente que as probabilidades sejam em função de

já que o exercício é genérico.
Também faz sentido a probabilidade de ocorrer um número negativo ser maior pois, quando retiramos a 1a. bola com um sinal restarão no saco mais bolas com o sinal oposto, (

), do que com o mesmo sinal da 1a. bola (
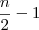
).
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidades - cálculo probabilidades e condicionada
por carlosmartins » Dom Set 21, 2014 18:58
- 0 Respostas
- 2950 Exibições
- Última mensagem por carlosmartins

Dom Set 21, 2014 18:58
Probabilidade
-
- probabilidades
 por edwilsoncrep » Qui Mar 04, 2010 19:28
por edwilsoncrep » Qui Mar 04, 2010 19:28
- 3 Respostas
- 3274 Exibições
- Última mensagem por edwilsoncrep

Qui Mar 04, 2010 19:49
Estatística
-
- Probabilidades!
por pferraz » Qui Out 27, 2011 22:53
- 3 Respostas
- 7062 Exibições
- Última mensagem por Russman

Qua Dez 23, 2015 22:04
Estatística
-
- Probabilidades
por matematicaead » Qua Nov 16, 2011 13:53
- 1 Respostas
- 2219 Exibições
- Última mensagem por Neperiano

Qua Nov 23, 2011 16:32
Estatística
-
- probabilidades
por cris_leite » Seg Jan 23, 2012 21:17
- 9 Respostas
- 5533 Exibições
- Última mensagem por fraol

Dom Jan 29, 2012 12:41
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


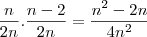
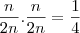
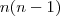 , pois a cada uma das
, pois a cada uma das 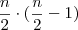
![2 \cdot \left[\frac{n}{2} \cdot (\frac{n}{2}-1)\right]=n \cdot (\frac{n}{2}-1)=\frac{n^2}{2}-n=\frac{n^2-2n}{2} 2 \cdot \left[\frac{n}{2} \cdot (\frac{n}{2}-1)\right]=n \cdot (\frac{n}{2}-1)=\frac{n^2}{2}-n=\frac{n^2-2n}{2}](/latexrender/pictures/70b6c77f8dd245696029b26d50bb88db.png)
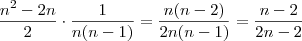
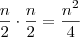
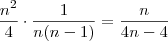
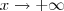 de ambas expressões cheguei a
de ambas expressões cheguei a  para o acontecimento
para o acontecimento  para o acontecimento
para o acontecimento 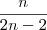
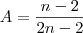
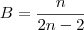
 já que o exercício é genérico.
já que o exercício é genérico. ), do que com o mesmo sinal da 1a. bola (
), do que com o mesmo sinal da 1a. bola (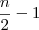 ).
).




