Olá,
Gostaria que me ajudassem, pois não estou conseguindo responder essa questão.
Verifique se existe o valor numérico para m da matriz M= [m 3], para que ela seja a matriz inversa de N=[-1 3]. justifique sua resposta. ..............continuação da matriz M [3 m].................continuação da matriz N [3 -1]
Já tentei fazer, mas não consegui. Eu comecei tentando tirar a matriz inversa de N, independente da matriz M e assim igualar os valores da inversa com a matriz M, mas não saiu nada. Por favor me ajude, perdi ponto por não conseguir responder essa atividade na matéria, acabei ficando curioso com o resultado, pois já procurei em tudo o que é site e não encontrei.
Att.


 é a seguinte:
é a seguinte: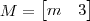 ?
?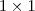 , ou seja, a própria unidade. A menos que a matriz
, ou seja, a própria unidade. A menos que a matriz  seja uma matriz coluna, não será possível multiplicá-las.
seja uma matriz coluna, não será possível multiplicá-las.

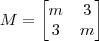 e
e 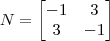 ?
?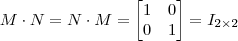 , que é a identidade no caso dois por dois. Seria necessário fazer ambas multiplicações, mas quando tratamos de matrizes quadradas, se existe uma inversa pela esquerda ou pela direita, segue diretamente que pelo outro lado também existe; assim basta efetuar um dos produtos e igualar a identidade. Com isso encontrará o valor de
, que é a identidade no caso dois por dois. Seria necessário fazer ambas multiplicações, mas quando tratamos de matrizes quadradas, se existe uma inversa pela esquerda ou pela direita, segue diretamente que pelo outro lado também existe; assim basta efetuar um dos produtos e igualar a identidade. Com isso encontrará o valor de  .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)