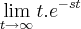
Onde s é um numero complexo.

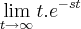

carvalhothg escreveu:Como calculo o limite abaixo, sem utilizar a regra de L'Hospital:
Onde s é um numero complexo.
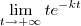 , com k real não nulo, sem usar a Regra de L'Hospital, só podemos aplicar uma análise qualitativa (não há simplificações algébricas).
, com k real não nulo, sem usar a Regra de L'Hospital, só podemos aplicar uma análise qualitativa (não há simplificações algébricas).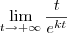 . Tanto o numerador quanto o denominador tendem para infinito. Entretanto, o crescimento do denominador é muito maior do que o crescimento do numerador. Nesse caso, teremos que
. Tanto o numerador quanto o denominador tendem para infinito. Entretanto, o crescimento do denominador é muito maior do que o crescimento do numerador. Nesse caso, teremos que 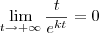 .
.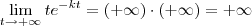 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.



