Danilo escreveu:Professor, então, posso colocar qualquer valor para

que o limite nunca vai dar um valor maior ou igual a 0,25, certo?
Você está fazendo confusão. Tome o exemplo que postei acima:

. Note, por exemplo, que

. Ou seja, os termos de uma sequência podem ser maiores (ou até menores) do que o seu valor limite. O importante é: para valores muito grandes de n, o valor de

está cada vez mais próximo de 0,25. No limite, quando
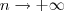
, temos que

.
Danilo escreveu:Só não sei como chegar a essa fórmula. Aqui no livro tem alguns teoremas, mas tá complicado de utilizar.
Para chegar nesses exemplos você não vai usar um teorema. Você vai criar esses exemplos com base na sua experiência calculando limites.
Imagine o seguinte exercício: dê um exemplo de uma função f tal que
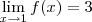
. Usando a sua experiência em calcular limites, você pode imaginar várias funções f que atendem essa exigência.
Agora a ideia é parecida. A diferença está apenas no fato de que a variável, no caso n, é natural e tende para o infinito. Isto é, temos limites nos quais aparece
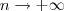
. Se você não estiver bem treinado em calcular limites desse tipo (isto é, limites no infinito), dificilmente vai conseguir criar os exemplos.
Danilo escreveu: Existe alguma 'maneira padrao' de encontrar essas 'fórmulas convergentes' ? Como chego lá?
Como disse acima, isso depende de sua experiência em calcular limites.
Por exemplo, você deve ter estudado que
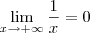
. Esse é um limite básico, que aprendemos tipicamente no início do estudo de limites no infinito.
Usando esse conhecimento (essa experiência), podemos por exemplo montar a seguinte sequência:
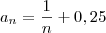
(aqui estou considerando que n começa em 1 e não em 0). Fica evidente então que
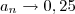
, já que

.
No caso do exemplo que exibi na mensagem anterior, note que

(lembrando que n é diferente de zero). Novamente eu usei aquele mesmo conhecimento básico, pois temos que

.
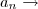 0,25
0,25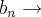 -2,31
-2,31![{c}_{n} \rightarrow \sqrt[]{2} {c}_{n} \rightarrow \sqrt[]{2}](/latexrender/pictures/d6bad020cee4761e226f507d10e90a5a.png)

 converge para 0,25 mas não sei com TOTAL CLAREZA o que isso quer dizer. Imagino que quanto maior o valor de n, mais de 0,25 a sequência se aproxima. certo? eu sei que uma sequencia constante é aquela que tem apenas um número... mas como assim uma sequencia constante tal que uma outra sequencia converge para um número?????
converge para 0,25 mas não sei com TOTAL CLAREZA o que isso quer dizer. Imagino que quanto maior o valor de n, mais de 0,25 a sequência se aproxima. certo? eu sei que uma sequencia constante é aquela que tem apenas um número... mas como assim uma sequencia constante tal que uma outra sequencia converge para um número?????

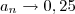 (ou que
(ou que  converge para 0,25) é o mesmo que dizer o seguinte:
converge para 0,25) é o mesmo que dizer o seguinte: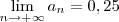
 .
.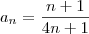 . Note que essa sequência não é constante e temos que
. Note que essa sequência não é constante e temos que 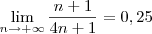

 n que o limite nunca vai dar um valor maior ou igual a 0,25, certo? Entendi. Só não sei como chegar a essa fórmula. Aqui no livro tem alguns teoremas, mas tá complicado de utilizar. Existe alguma 'maneira padrao' de encontrar essas 'fórmulas convergentes' ? Como chego lá? Obrigado aí ^^
n que o limite nunca vai dar um valor maior ou igual a 0,25, certo? Entendi. Só não sei como chegar a essa fórmula. Aqui no livro tem alguns teoremas, mas tá complicado de utilizar. Existe alguma 'maneira padrao' de encontrar essas 'fórmulas convergentes' ? Como chego lá? Obrigado aí ^^ que o limite nunca vai dar um valor maior ou igual a 0,25, certo?
que o limite nunca vai dar um valor maior ou igual a 0,25, certo? . Note, por exemplo, que
. Note, por exemplo, que  . Ou seja, os termos de uma sequência podem ser maiores (ou até menores) do que o seu valor limite. O importante é: para valores muito grandes de n, o valor de
. Ou seja, os termos de uma sequência podem ser maiores (ou até menores) do que o seu valor limite. O importante é: para valores muito grandes de n, o valor de 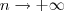 , temos que
, temos que  .
.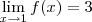 . Usando a sua experiência em calcular limites, você pode imaginar várias funções f que atendem essa exigência.
. Usando a sua experiência em calcular limites, você pode imaginar várias funções f que atendem essa exigência.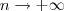 . Se você não estiver bem treinado em calcular limites desse tipo (isto é, limites no infinito), dificilmente vai conseguir criar os exemplos.
. Se você não estiver bem treinado em calcular limites desse tipo (isto é, limites no infinito), dificilmente vai conseguir criar os exemplos.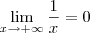 . Esse é um limite básico, que aprendemos tipicamente no início do estudo de limites no infinito.
. Esse é um limite básico, que aprendemos tipicamente no início do estudo de limites no infinito.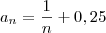 (aqui estou considerando que n começa em 1 e não em 0). Fica evidente então que
(aqui estou considerando que n começa em 1 e não em 0). Fica evidente então que  .
. (lembrando que n é diferente de zero). Novamente eu usei aquele mesmo conhecimento básico, pois temos que
(lembrando que n é diferente de zero). Novamente eu usei aquele mesmo conhecimento básico, pois temos que  .
.![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) ?^ Valeu !
?^ Valeu ! ?
?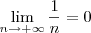 . Com base no que eu já expliquei anteriormente, fica fácil exibir pelo menos um exemplo tal que
. Com base no que eu já expliquei anteriormente, fica fácil exibir pelo menos um exemplo tal que 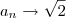 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)