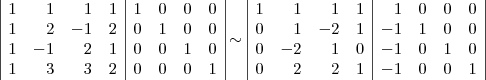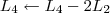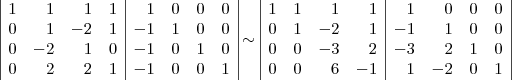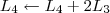Rhyu escreveu:Bom estou com dificuldades em achar a matriz inversa em matrizes 4x4 não sei por onde eu começo a zerar as colunas como nesse exercicio
I1 1 1 1I Linha 1 (1,1,1,1)
I1 2 -1 2I Linha 2 (1,2,-1,2)
I1-1 2 1I Linha 3 (1,-1,2,1)
I1 3 3 2I Linha 4 (1,3,3,2)
Como eu acho a inversa dessa aplicando o método de Gauss Jordan, gostaria de saber também qual a ordem eu devo seguir para zerar os termos.
Se você já sabe determinar a inversa de uma matriz 3 por 3 usando o método de Gauss Jordan, então basta aplicar a mesma ideia para uma matriz 4 por 4.
Siga basicamente os seguintes passos:
1) transformar em 0 todos os elementos abaixo de

;
2) transformar em 0 todos os elementos abaixo de
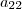
;
3) transformar em 0 todos os elementos abaixo de
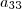
;
4) transformar em 0 todos os elementos acima de
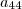
;
5) transformar em 0 todos os elementos acima de
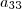
;
6) transformar em 0 todos os elementos acima de
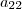
;
7) transformar em 1 todos os elementos na diagonal principal.
Veja o início do processo.
Passo 1)



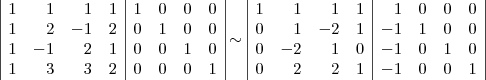
Passo 2)

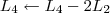
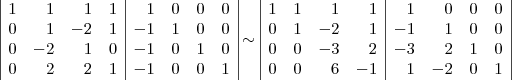
Passo 3)
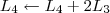

Agora tente terminar o exercício.


 ;
;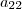 ;
;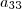 ;
;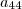 ;
;