paola-carneiro escreveu:Essa questão é da atividade avaliativa que vai ser pontuada:
Dada a função

, calcule:
a) de modo que f(x)= f(1)
b)m, de modo que f(m+1)=5.
paola-carneiro escreveu:Na letra a, resolvi a equação com Báskara, e o delta deu -4, mas não existe raiz negativa. Mas, se eu ignorar o sinal, a solução fica S= {1,3} igual a resposta certa.
Mas, é claro que o jeito de calcular tá errado, pois ignorei um sinal e não usei o que diz o enunciado da letra ( que f(x)= f(1) ).
Usando o que diz no item a), precisamos resolver:
f(x) = f(1)
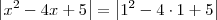
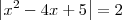
Para resolver essa equação modular, temos que resolver duas equações:
(i)

;
(ii)

.
Agora resolva essas equações. A primeira terá solução

. Já a segunda não terá solução real, isto é, no conjunto dos reais temos que

. A solução da equação modular original é a união dessas duas soluções. Temos então que
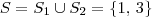
.
paola-carneiro escreveu:e a b, não sei como resolver.
Usando o que diz no item b), precisamos resolver:
f(m + 1) = 5
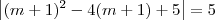

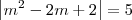
Para resolver essa equação modular, temos que resolver duas equações:
(i)

;
(ii)

.
Agora tente terminar o exercício. Lembre-se que a solução da equação modular original será a união das soluções dessas duas equações.
 , calcule:
, calcule:

 , calcule:
, calcule: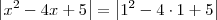
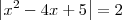
 ;
; .
. . Já a segunda não terá solução real, isto é, no conjunto dos reais temos que
. Já a segunda não terá solução real, isto é, no conjunto dos reais temos que  . A solução da equação modular original é a união dessas duas soluções. Temos então que
. A solução da equação modular original é a união dessas duas soluções. Temos então que 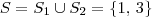 .
.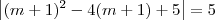

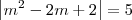
 ;
; .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.