 por LuizAquino » Sex Abr 06, 2012 00:39
por LuizAquino » Sex Abr 06, 2012 00:39
Guilherme Carvalho escreveu:![\int_{} \sqrt[]{{x}^{2}-2x}dx \int_{} \sqrt[]{{x}^{2}-2x}dx](/latexrender/pictures/e71e5eb610a390828c246aa13037b68d.png)
![\int_{} \ x \left( \sqrt[]{1 - {x}^{4}}\right)dx \int_{} \ x \left( \sqrt[]{1 - {x}^{4}}\right)dx](/latexrender/pictures/a4b039386152f75418525ed90a3b31b4.png)
Guilherme Carvalho escreveu:Não consegui resolver essas integrais alquém pode me ajudar, por favor...
DicasQuanto a primeira, note que:
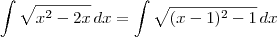
Agora use a substituição trigonométrica
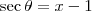
.
Quanto a segunda, note que:
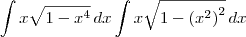
Agora use a substituição trigonométrica
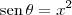
.
Tente terminar o exercício aplicando essas dicas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8837 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2811 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2440 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2524 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2138 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{} \sqrt[]{{x}^{2}-2x}dx \int_{} \sqrt[]{{x}^{2}-2x}dx](/latexrender/pictures/e71e5eb610a390828c246aa13037b68d.png)
![\int_{} \ x \left( \sqrt[]{1 - {x}^{4}}\right)dx \int_{} \ x \left( \sqrt[]{1 - {x}^{4}}\right)dx](/latexrender/pictures/a4b039386152f75418525ed90a3b31b4.png)

![\int_{} \sqrt[]{{x}^{2}-2x}dx \int_{} \sqrt[]{{x}^{2}-2x}dx](/latexrender/pictures/e71e5eb610a390828c246aa13037b68d.png)
![\int_{} \ x \left( \sqrt[]{1 - {x}^{4}}\right)dx \int_{} \ x \left( \sqrt[]{1 - {x}^{4}}\right)dx](/latexrender/pictures/a4b039386152f75418525ed90a3b31b4.png)

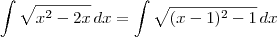
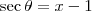 .
.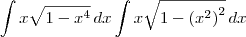
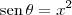 .
.