Estou aqui estudando Inequações!
Mas estou com uma dúvida, sobre inequações equivalentes!
Exemplo: As inequações
 e
e  são inequações equivalentes, é uma pergunta, meu teclado não tem como digitar o ponto de interrogação!
são inequações equivalentes, é uma pergunta, meu teclado não tem como digitar o ponto de interrogação!Para isso aplicamos os princípios das desigualdades.

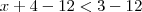 ------------------------------- subtraindo 12 de cada membro.
------------------------------- subtraindo 12 de cada membro.
Partindo de
 obtemos
obtemos  . Dizemos que estas inequações são equivalentes. Elas têm as mesmas soluções num mesmo conjunto universo.
. Dizemos que estas inequações são equivalentes. Elas têm as mesmas soluções num mesmo conjunto universo.Minha dúvida, como sei que tenho que subtrair 12 de cada membro da desigualdade. Ou simplesmente adiciono ou subtraio qualquer número que venha a minha mente, desde que faço isso nos dois membros da desigualdade, dessa forma obtendo uma desigualdade equivalente.
Não entendi essa explicação, e o livro não deixa isso claro.
Obrigado a todos.


 tal que
tal que 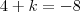 . Daí,
. Daí, 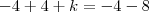 e
e  . Como queremos manter a desigualdade, fazemos
. Como queremos manter a desigualdade, fazemos  , o que nos leva a
, o que nos leva a 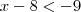 .
.

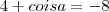 . Subtraímos quatro para encontrar o valor que queremos, logo
. Subtraímos quatro para encontrar o valor que queremos, logo 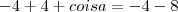 . Daí, isolamos coisa e descobrimos seu valor, que é
. Daí, isolamos coisa e descobrimos seu valor, que é  .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)