Resolvi esse problema, encontrando a solução!
Mas o livro resolveu de forma diferente da forma como resolvi, dessa forma me deixando em dúvida!
Quero somente entender como o livro resolveu, pois consegui encontrar o resultado correto.
Juca está apaixonado! Para ver a namorada, ele faz uma longa viagem: 350 km a cada encontro. Numa de suas viagens, após alguns quilômetros, ele parou para um cafezinho e ainda percorreu o triplo do que já havia percorrido para chegar á cidade de sua namorada. Quantos quilômetros ele percorreu após o cafezinho.
Resolução:
a ------------------------- percurso antes do cafezinho
3a ------------------------ percurso após o cafezinho
a + 3a = 350km
4a = 350km
a =

a = 87, 5 km
87,5 km --------------------------- percurso antes do cafezinho
 = 262,5 km
= 262,5 km262,5 km -------------------------- percurso após o cafezinho
Resolução do livro:
x ----------------- Número de quilômetros percorridos após o cafezinho.
x ------------------ Número racional positivo : U = Q+
 -------------- x é o triplo de
-------------- x é o triplo de  portanto
portanto  é a parte percorrida antes do cafezinho.
é a parte percorrida antes do cafezinho. + x = 350 ------------------------- Equação do problema.
+ x = 350 ------------------------- Equação do problema.Não entendi! como assim x é o triplo de
 , portanto
, portanto  é a parte percorrida antes do cafezinho.
é a parte percorrida antes do cafezinho.

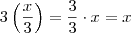 . Isto é equivalente a dizer que
. Isto é equivalente a dizer que  .
.

